If an electron drops from n = 4 to n = 2 in Li2+ then would the released wavelength lie in the visible region?
To determine whether the wavelength released when an electron drops from n = 4 to n = 2 in Li²⁺ lies in the visible region, we can follow these steps:
Step 1: Identify the formula for wavelength in hydrogen-like atoms
The wavelength of light emitted during an electron transition in hydrogen-like atoms can be calculated using the formula:
1λ=RZ2(1n21−1n22)
where:
- λ is the wavelength,
- R is the Rydberg constant (R=109678cm−1),
- Z is the atomic number,
- n1 is the lower energy level,
- n2 is the higher energy level.
Step 2: Determine the values for Li²⁺
For lithium ion (Li²⁺):
- The atomic number Z=3 (since lithium has an atomic number of 3).
- The electron transition is from n2=4 to n1=2.
Step 3: Substitute the values into the formula
Substituting the values into the formula:
1λ=109678×32(122−142)
Calculating 32=9, 22=4, and 42=16:
1λ=109678×9(14−116)
Step 4: Simplify the expression
Now, calculate 14−116:
14=416thus14−116=416−116=316
Substituting back:
1λ=109678×9×316
Step 5: Calculate 1λ
Calculating:
1λ=109678×9×316=185081cm−1
Step 6: Find λ
Taking the reciprocal to find λ:
λ=1185081cm
Converting to meters:
λ=1185081×10−2m=5.403×10−8m
Step 7: Convert to Angstroms
To convert meters to Angstroms (1 m = 1010 Å):
λ=5.403×10−8m×1010Å/m=540.3Å
Step 8: Determine if it lies in the visible region
The visible region of the spectrum is approximately from 4000 Å to 7000 Å. Since 540.3Å is less than 4000 Å, it does not lie in the visible region.
Conclusion
The wavelength released when an electron drops from n = 4 to n = 2 in Li²⁺ does not lie in the visible region.
---
The wavelength of light emitted during an electron transition in hydrogen-like atoms can be calculated using the formula:
1λ=RZ2(1n21−1n22)
where:
- λ is the wavelength,
- R is the Rydberg constant (R=109678cm−1),
- Z is the atomic number,
- n1 is the lower energy level,
- n2 is the higher energy level.
For lithium ion (Li²⁺):
- The atomic number Z=3 (since lithium has an atomic number of 3).
- The electron transition is from n2=4 to n1=2.
Substituting the values into the formula:
1λ=109678×32(122−142)
Calculating 32=9, 22=4, and 42=16:
1λ=109678×9(14−116)
Now, calculate 14−116:
14=416thus14−116=416−116=316
Substituting back:
1λ=109678×9×316
Calculating:
1λ=109678×9×316=185081cm−1
Taking the reciprocal to find λ:
λ=1185081cm
Converting to meters:
λ=1185081×10−2m=5.403×10−8m
To convert meters to Angstroms (1 m = 1010 Å):
λ=5.403×10−8m×1010Å/m=540.3Å
The visible region of the spectrum is approximately from 4000 Å to 7000 Å. Since 540.3Å is less than 4000 Å, it does not lie in the visible region.
The wavelength released when an electron drops from n = 4 to n = 2 in Li²⁺ does not lie in the visible region.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - IN-CHAPTER EXERCISE-A10videos
STRUCTURE OF ATOM
- BOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - IN-CHAPTER EXERCISE-B9videos
STRUCTURE OF ATOM
- BOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - Example19videos
STRUCTURE OF ATOM
- BOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY-IIEXERCISE - JEE Advanced (Archive)43videos
STOICHIOMETRY-II
- BOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE9videos
SURFACE CHEMISTRY
Similar Questions
In a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
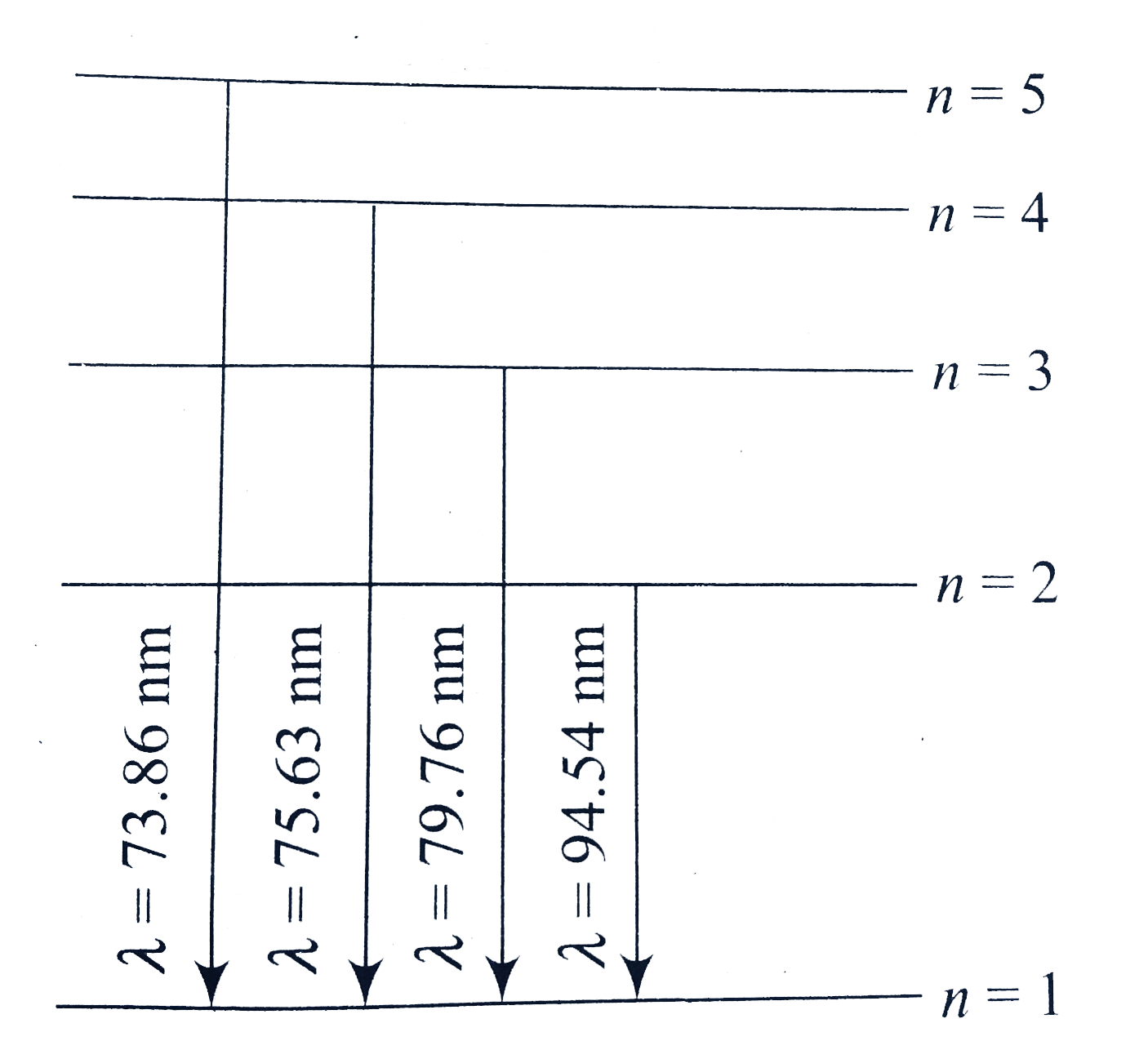
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearlyView SolutionWhen an electron do transition from n = 4 to n = 2, then emitted line in spectrum will be:
View SolutionIn excited H atom when electron drop from n=4,5,6 to n=1, there is emission of
View SolutionThe electron energy in hydrogen atom is given by En=−2.18×10−18n2J. Calculate the energy required to remove an electron completely from the n=2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
View SolutionThe atomic spectrum of Li+2 ion arises due to the transition of an electron from n2 to n1 if n1+n2=4 and (n2−n1) =2 then the wavelength of 3rd line of this series in Li+2 ion will be
View SolutionAssertion :The spectral series 'Blamer' of the of the hydrogen atom lies in the visible region of the electromagnetic spetrum
Reason :Wavelength of light in the visible region lies in the range of 400 nm to 700 nmView SolutionIn excited H atom, when electron drop from n=4,5,6 to n=1, there is emission of
View SolutionWhich transition in Li2+ would have the same wavelength as the 2→4 transition in He+ ion ?
View SolutionIn excited H atom, when electron drop from n = 4, 5, 6 to n = 1, there is emission of:
View SolutionThe energy of nth orbit is given by
En=−Rhcn2
When electron jumpsfrom one orbit to another orbit then wavelength associated with the radiation is given by
1λ=RZ2(1n21−1n22)
The series that belongs to visible region isView Solution

