Spin magnetic moment of Xn+(Z=26) is √24B.M. Hence number of unpaired electrons and value of n respectively are:
4,2
2,4
3,1
0,2
The correct Answer is:A
To solve the problem, we need to determine the number of unpaired electrons and the charge (n) of the ion Xn+ with atomic number Z=26 (which corresponds to iron, Fe). The spin magnetic moment is given as √24B.M..
1. Understanding the Spin Magnetic Moment Formula:
The formula for the spin magnetic moment (μ) is given by:
μ=√n(n+2)B.M.
where n is the number of unpaired electrons.
2. Setting Up the Equation:
We know from the problem that:
μ=√24B.M.
Therefore, we can equate:
√n(n+2)=√24
3. Squaring Both Sides:
To eliminate the square root, we square both sides:
n(n+2)=24
4. Rearranging the Equation:
Rearranging gives us a quadratic equation:
n2+2n−24=0
5. Factoring the Quadratic Equation:
We can factor the quadratic:
(n+6)(n−4)=0
This gives us two possible solutions for n:
n=−6orn=4
Since n must be a non-negative integer, we take:
n=4
6. Determining the Charge (n):
The atomic number Z=26 corresponds to iron (Fe), whose electronic configuration is:
Fe: (Ar)4s23d6
In the case of the Fe2+ ion, two electrons are removed (typically from the 4s orbital first), leading to:
Fe2+:(Ar)4s03d6
In this configuration, the 3d subshell has 6 electrons, which can be arranged to show 4 unpaired electrons.
7. Conclusion:
Thus, the number of unpaired electrons is 4 and the charge n of the ion is 2 (since it is Fe2+).
Final Answer:
The number of unpaired electrons and the value of n respectively are:
- Number of unpaired electrons: 4
- Value of n: 2
The formula for the spin magnetic moment (μ) is given by:
μ=√n(n+2)B.M.
where n is the number of unpaired electrons.
We know from the problem that:
μ=√24B.M.
Therefore, we can equate:
√n(n+2)=√24
To eliminate the square root, we square both sides:
n(n+2)=24
Rearranging gives us a quadratic equation:
n2+2n−24=0
We can factor the quadratic:
(n+6)(n−4)=0
This gives us two possible solutions for n:
n=−6orn=4
Since n must be a non-negative integer, we take:
n=4
The atomic number Z=26 corresponds to iron (Fe), whose electronic configuration is:
Fe: (Ar)4s23d6
In the case of the Fe2+ ion, two electrons are removed (typically from the 4s orbital first), leading to:
Fe2+:(Ar)4s03d6
In this configuration, the 3d subshell has 6 electrons, which can be arranged to show 4 unpaired electrons.
Thus, the number of unpaired electrons is 4 and the charge n of the ion is 2 (since it is Fe2+).
The number of unpaired electrons and the value of n respectively are:
- Number of unpaired electrons: 4
- Value of n: 2
Topper's Solved these Questions
- STRUCTURE OF ATOMBOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - IN-CHAPTER EXERCISE-E
12 Videos
- STOICHIOMETRY-IIBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY-IIEXERCISE - JEE Advanced (Archive)
43 Videos
- SURFACE CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE
9 Videos
Similar Questions
The magnetic moment of Mx+ (atomic number =25 is √15BM .The number of unpaired electron and the value of x respectively are
View SolutionNumber of unpaired electrons in Fe3+ (Z = 26) is
View Solution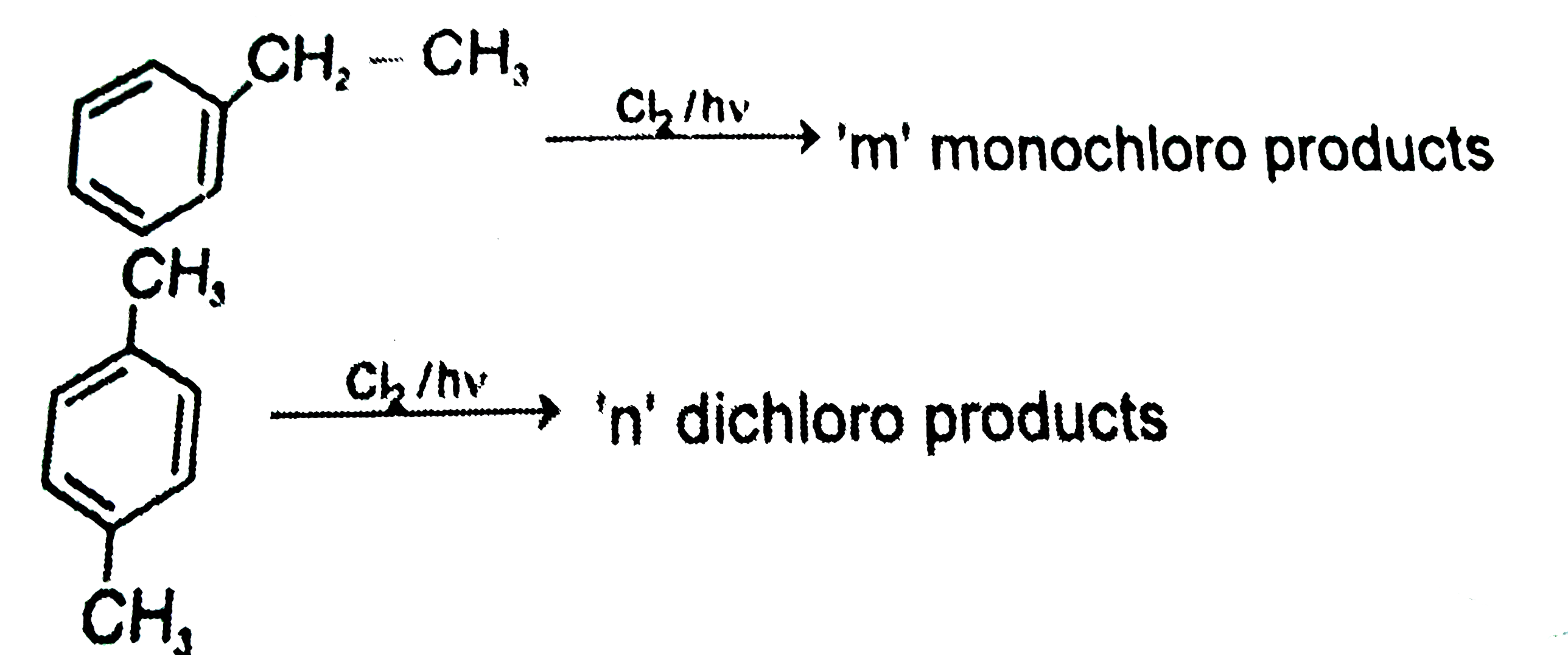
The value of m and n are respectively :
View Solution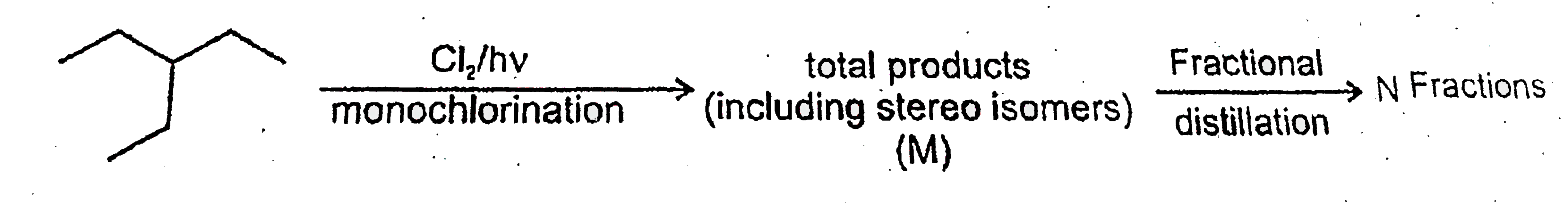
The value of M and N are respectively.
View SolutionHow is the magnetic moment of a species related to the number of unpaired electrons ?
View SolutionA compound of a metal ion MX+(z=24) has a spin only magnetic moment of √15B.M. . The number of unpaired electrons in the compound are
View SolutionAzimuthal quantum number (l) :
It describes the shape of electron cloud and the number of subshells in a shell. It can have value from 0 to (n-1)
Value of l0123subshellspdr
Number of orbitals in a subshell =2l+1
Orbital angular momentum L=h2π√l(l+1)=ħ√l(l+1) [ħ=h2π]
Magnetic quantum number (m) :
It describes the orientations of the subshells . It can have values from -l to +l including zero, i.e. , total (2l+1) values . Each value corresponds to an orbital. s-subshell has one orbital , p-subshell three orbitals (px,pyandpz) , d-subshell five orbitals (dxy,dyz,dx2−y2,d2z) and f-subshell has seven orbitals.
Spin quantum number (s) :
It describes the spin of the electron. It has values +1/2 and -1/2 . Signifies clockwise spinning and anticlockwise rotation of electron about its own axis.
Spin of the electron produces angular momentum equal to S=√s(s+1)h2π where s=+12
Total spin of an atom =+n2 or −n2 (where n is the number of unpaired electron )
The magnetic moment of an atom
μs=√n(n+2) B.M. n=number of unpaired electrons
B.M. (Bohr magneton)
Orbital angular momentum of an electron is √3hπ then the number of orientations of this orbital in spaces are :
View SolutionThe magnetic moment of a transition metal ion is 3.87BM. The number of unpaired electrons present in it is
View SolutionThe spin only magnetic moment of transition metal ion found to be 5.92 BM. The number of unpaired electrons present in the species is :
View SolutionThe spin only magnetic moment of transition metal ion found to be 5.92 BM. The number of unpaired electrons present in the species is :
View Solution
