A cylinder with a movable piston is filled at 25∘C with a gas that occupies a volume of 30.5cm3. If the maximum capacity of the cylinder is 45.8cm3, what is the highest temperature to which the cylinder can be heated at constant pressure without having the piston come out?
50∘C
147.5∘C
174.5∘C
120∘C
The correct Answer is:C
To solve the problem, we will use the relationship between volume and temperature for a gas at constant pressure, which is given by Charles's Law. The formula we will use is:
V1T1=V2T2
Where:
- V1 = initial volume of the gas
- T1 = initial temperature of the gas (in Kelvin)
- V2 = maximum volume of the gas
- T2 = final temperature of the gas (in Kelvin)
Step 1: Convert the initial temperature from Celsius to Kelvin
To convert Celsius to Kelvin, we use the formula:
T(K)=T(°C)+273.15
Given T1=25°C:
T1=25+273.15=298.15K
Step 2: Identify the volumes
From the problem statement:
- V1=30.5cm3
- V2=45.8cm3
Step 3: Rearrange the Charles's Law equation to solve for T2
We can rearrange the equation to find T2:
T2=V2⋅T1V1
Step 4: Substitute the known values into the equation
Now we can substitute V2, T1, and V1 into the equation:
T2=45.8cm3⋅298.15K30.5cm3
Step 5: Calculate T2
Performing the calculation:
T2=45.8⋅298.1530.5≈455.15K
Step 6: Convert T2 back to Celsius
To convert back to Celsius:
T2(°C)=T2(K)−273.15
T2(°C)=455.15−273.15≈182.0°C
Final Answer
The highest temperature to which the cylinder can be heated at constant pressure without having the piston come out is approximately 182.0°C.
- V1 = initial volume of the gas
- T1 = initial temperature of the gas (in Kelvin)
- V2 = maximum volume of the gas
- T2 = final temperature of the gas (in Kelvin)
To convert Celsius to Kelvin, we use the formula:
T(K)=T(°C)+273.15
Given T1=25°C:
T1=25+273.15=298.15K
From the problem statement:
- V1=30.5cm3
- V2=45.8cm3
We can rearrange the equation to find T2:
T2=V2⋅T1V1
Now we can substitute V2, T1, and V1 into the equation:
T2=45.8cm3⋅298.15K30.5cm3
Performing the calculation:
T2=45.8⋅298.1530.5≈455.15K
To convert back to Celsius:
T2(°C)=T2(K)−273.15
T2(°C)=455.15−273.15≈182.0°C
The highest temperature to which the cylinder can be heated at constant pressure without having the piston come out is approximately 182.0°C.
Topper's Solved these Questions
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-D
10 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-E
9 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-B
10 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IMPECCABLE
50 Videos
- STOICHIOMETRY - IBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - JEE Advanced (Archive)
31 Videos
Similar Questions
The piston cylinder arrangement shown contains a diatomic gas at temperature 300 K The cross sectinal area of the cylinder is 1m2. Initially the height of the piston above th base of the cyclinder is 1 m. The temperature is now raised to 400 K at constant pressure. There is no heat loss in the process..
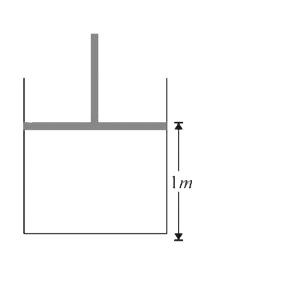
Find the new height (in m) of the piston above the base of the cylinder.
View SolutionA cyclinder with a movable piston contains 3mols of hydrogen at standard temperature and pressure. The walls of the cyclinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increases, if the gas is compressed to half its original volume? Given γ=1.4.
View SolutionA sample of gas is found to occupy a volume of 900cm3 at 27∘C. Calculate the temperature at which it will occupy a volume of 300cm3, provided the pressure is kept constant.
View SolutionAt 3 atm and 17∘C a gas cylinder has a volume of 10 litre. If the temperature of cylinder is increased to 47∘C, how many litres of air measured at 47∘C and pressure of 1 atm should be let out to restore the pressure to 3 atm at 47∘C ?
View SolutionA sample of a gas occupies 650.0 cm at 100∘C. At what temperature the gas will occupy a volume of 1050.0cm3 if the pressure is kept constant ?
View SolutionA gas occupies a volume of 250cm3 at 745 torr and 25∘C . What additional pressure is required to reduce the volume of the gas to 200cm3 at the same temperature ?
View SolutionFind the maximum volume of the cylinder which can be inscribed in a sphere of radius 3√3cm (Leave the answer in terms of π)
View SolutionShow that the maximum volume of the cylinder which can be inscribed in a sphere of radius 5√3cm is 500πcm3.
View SolutionA cylinder has a movable piston on its top. The piston has a mass of 7 kg and an area of 6×10−4m2. The piston can slide up and down, keeping the pressure of the ideal gas enclosed in the cylinder constant. What is the work done if the temperature of 0.5 mol of the gas in raised from 30∘C to 250∘C?[R=8.31Jmol−1K−1]
View SolutionA container is closed by a movable piston. We supply heat to gas inside container. Due to heating, piston is displaced by 5 cm. cross section area of cylinder is 40 cm2 and heat supplied to gas is 40 joules. The change in internal energy is

View Solution
