Molecular weight of a gas that diffuses twice as rapidly as the gas with molecular weight 64 is
16
8
64
6.4
The correct Answer is:A
To solve the problem of finding the molecular weight of a gas that diffuses twice as rapidly as a gas with a molecular weight of 64, we can use Graham's law of effusion. Here’s a step-by-step solution:
Step 1: Understand Graham's Law
Graham's law states that the rate of diffusion of a gas is inversely proportional to the square root of its molar mass. Mathematically, this can be expressed as:
r1r2=√M2M1
where:
- r1 = rate of diffusion of gas 1
- r2 = rate of diffusion of gas 2
- M1 = molar mass of gas 1
- M2 = molar mass of gas 2
Step 2: Set Up the Problem
In this problem, we know that gas 2 diffuses twice as rapidly as gas 1. Therefore, we can express this relationship as:
r2=2r1
Step 3: Substitute into Graham's Law
Substituting r2 into Graham's law gives us:
r12r1=√M2M1
This simplifies to:
12=√M2M1
Step 4: Square Both Sides
To eliminate the square root, we square both sides:
(12)2=M2M1
This simplifies to:
14=M2M1
Step 5: Substitute Known Values
We know that the molar mass of gas 1 (M1) is 64. Therefore, we substitute this value into the equation:
14=M264
Step 6: Solve for M2
To find M2, we multiply both sides by 64:
M2=64×14
Calculating this gives:
M2=16
Conclusion
Thus, the molecular weight of the gas that diffuses twice as rapidly as the gas with a molecular weight of 64 is 16.
Graham's law states that the rate of diffusion of a gas is inversely proportional to the square root of its molar mass. Mathematically, this can be expressed as:
- r1 = rate of diffusion of gas 1
- r2 = rate of diffusion of gas 2
- M1 = molar mass of gas 1
- M2 = molar mass of gas 2
In this problem, we know that gas 2 diffuses twice as rapidly as gas 1. Therefore, we can express this relationship as:
Substituting r2 into Graham's law gives us:
To eliminate the square root, we square both sides:
We know that the molar mass of gas 1 (M1) is 64. Therefore, we substitute this value into the equation:
To find M2, we multiply both sides by 64:
Thus, the molecular weight of the gas that diffuses twice as rapidly as the gas with a molecular weight of 64 is 16.
Topper's Solved these Questions
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-H
9 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-I
10 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- STATES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IMPECCABLE
50 Videos
- STOICHIOMETRY - IBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - JEE Advanced (Archive)
31 Videos
Similar Questions
Molecular weight of DNA in yeast is
View Solution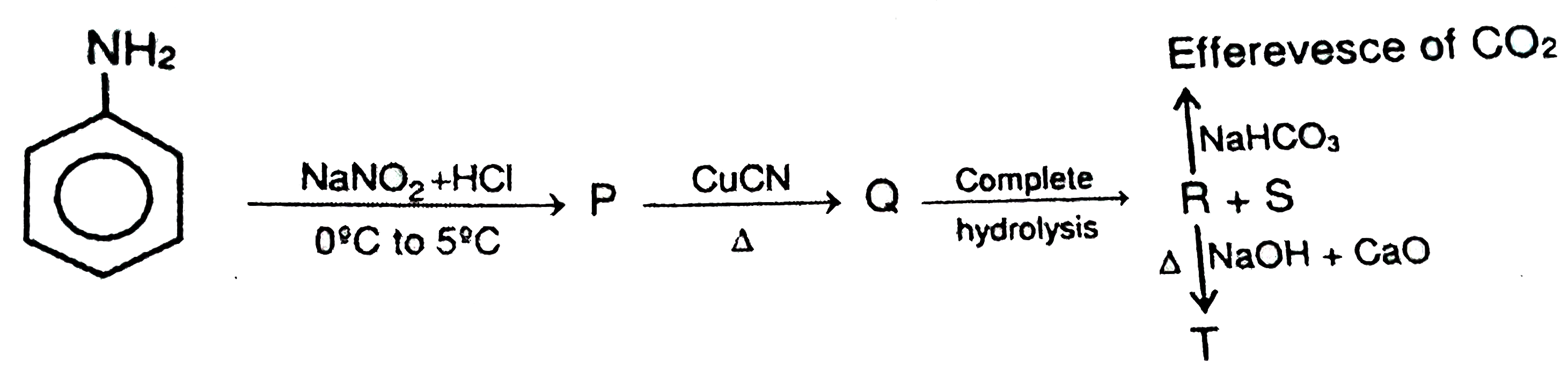
Molecular weight of T will be:
View Solution
Molecular weight of T will be:
View SolutionMolecular weight of nitric acid.
View Solution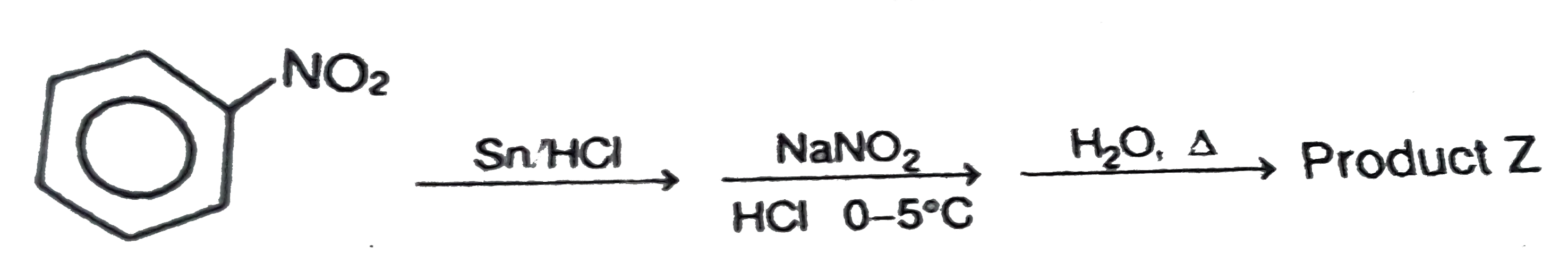
Find the molecular weight of Z.
View Solution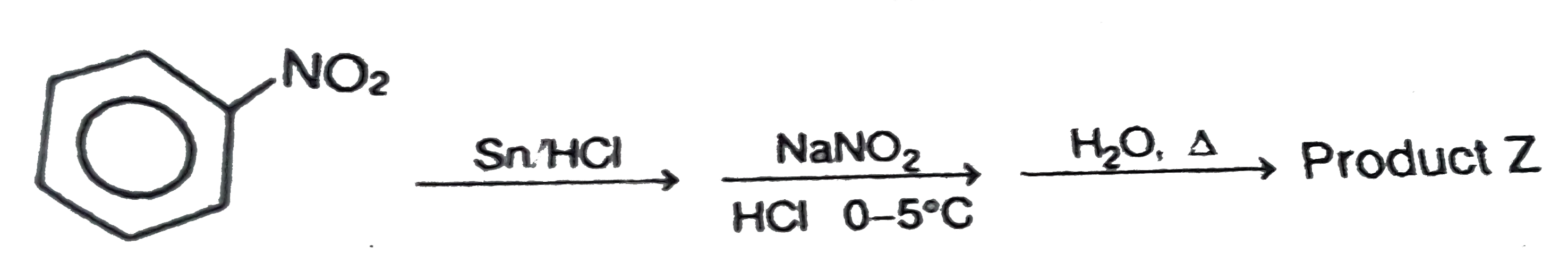
Find the molecular weight of Z.
View SolutionMolecular weight of an organic acid is given by:
View SolutionCalculate the molecular weight of a gas X which diffuses four times as fast as another gas Y, which in turn diffuses twice as fast as another Z. Molecular weight of the gas Z is 128.
View SolutionCalculate the molecular weight of a gas which diffuses four times as fast as another gas Y, which in turn diffuses twice as fast as another gas Z [All under identical conditions]. Molecules weight of Z is 128.
View SolutionA gas diffuses four times as quickly as oxygen. The molecular weight of the gas is
View Solution
