Which of the following is correct?
Crystal systemAxial distanceAxial anglesExamples(1)Cubica≠b=cα=β≠γ=90∘Cu,KCI(2)Monoclinica≠b=cα=β=γ=90∘PbCrO2,PbCrO4(3)Rhombohedrala=b=cα=β=γ≠90∘CaCO3,NaNO3(4)Triclinica=b=cα≠β=γ≠90∘K2Cr2O7,CuSO4,5H2O
The correct Answer is:C
To determine which of the given options regarding crystal systems is correct, we will analyze each option based on the properties of the respective crystal systems.
1. Cubic System:
- Axial Distances: In a cubic system, all axial distances are equal, i.e., a=b=c.
- Axial Angles: All axial angles are equal to 90∘, i.e., α=β=γ=90∘.
- Examples: Common examples include Cu and KCl.
- Conclusion: The statement in the question is incorrect because it states a≠b and β≠γ.
2. Monoclinic System:
- Axial Distances: In a monoclinic system, the axial distances are unequal, i.e., a≠b≠c.
- Axial Angles: The angles are such that α=γ and β≠90∘.
- Examples: Examples include PbCrO2 and PbCrO4.
- Conclusion: This option is also incorrect as it misrepresents the relationship between the axial angles.
3. Rhombohedral System:
- Axial Distances: In a rhombohedral system, all axial distances are equal, i.e., a=b=c.
- Axial Angles: The angles are equal, i.e., α=β=γ, but they are not equal to 90∘.
- Examples: Examples include CaCO3 and NaNO3.
- Conclusion: This option is correct as it accurately describes the properties of the rhombohedral system.
4. Triclinic System:
- Axial Distances: In a triclinic system, all axial distances are unequal, i.e., a≠b≠c.
- Axial Angles: All angles are unequal, i.e., α≠β≠γ, and none are 90∘.
- Examples: Examples include K2Cr2O7 and CuSO4·5H2O.
- Conclusion: This option is incorrect as it does not match the properties of the triclinic system.
Final Answer:
The correct option is Option 3: Rhombohedral.
- Axial Distances: In a cubic system, all axial distances are equal, i.e., a=b=c.
- Axial Angles: All axial angles are equal to 90∘, i.e., α=β=γ=90∘.
- Examples: Common examples include Cu and KCl.
- Conclusion: The statement in the question is incorrect because it states a≠b and β≠γ.
- Axial Distances: In a monoclinic system, the axial distances are unequal, i.e., a≠b≠c.
- Axial Angles: The angles are such that α=γ and β≠90∘.
- Examples: Examples include PbCrO2 and PbCrO4.
- Conclusion: This option is also incorrect as it misrepresents the relationship between the axial angles.
- Axial Distances: In a rhombohedral system, all axial distances are equal, i.e., a=b=c.
- Axial Angles: The angles are equal, i.e., α=β=γ, but they are not equal to 90∘.
- Examples: Examples include CaCO3 and NaNO3.
- Conclusion: This option is correct as it accurately describes the properties of the rhombohedral system.
- Axial Distances: In a triclinic system, all axial distances are unequal, i.e., a≠b≠c.
- Axial Angles: All angles are unequal, i.e., α≠β≠γ, and none are 90∘.
- Examples: Examples include K2Cr2O7 and CuSO4·5H2O.
- Conclusion: This option is incorrect as it does not match the properties of the triclinic system.
The correct option is Option 3: Rhombohedral.
Topper's Solved these Questions
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - EXERCISE -C
10 Videos
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - EXERCISE-D
10 Videos
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - EXERCISE - A
10 Videos
- SURFACE CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE
9 Videos
- THEORY OF SOLUTIONSBOOK - VMC MODULES ENGLISHCHAPTER - THEORY OF SOLUTIONSEXERCISE - JEE Advanced (Archive)
31 Videos
Similar Questions
Knowledge Check
The crystal system for which a≠b≠candα=β=γ=90∘ is said to be
ACubicBTetragonalCOrthorhombicDHexagonal
Example of unit cell with crystallographic dimensions
a≠b≠c,α=β=γ=90∘ is :
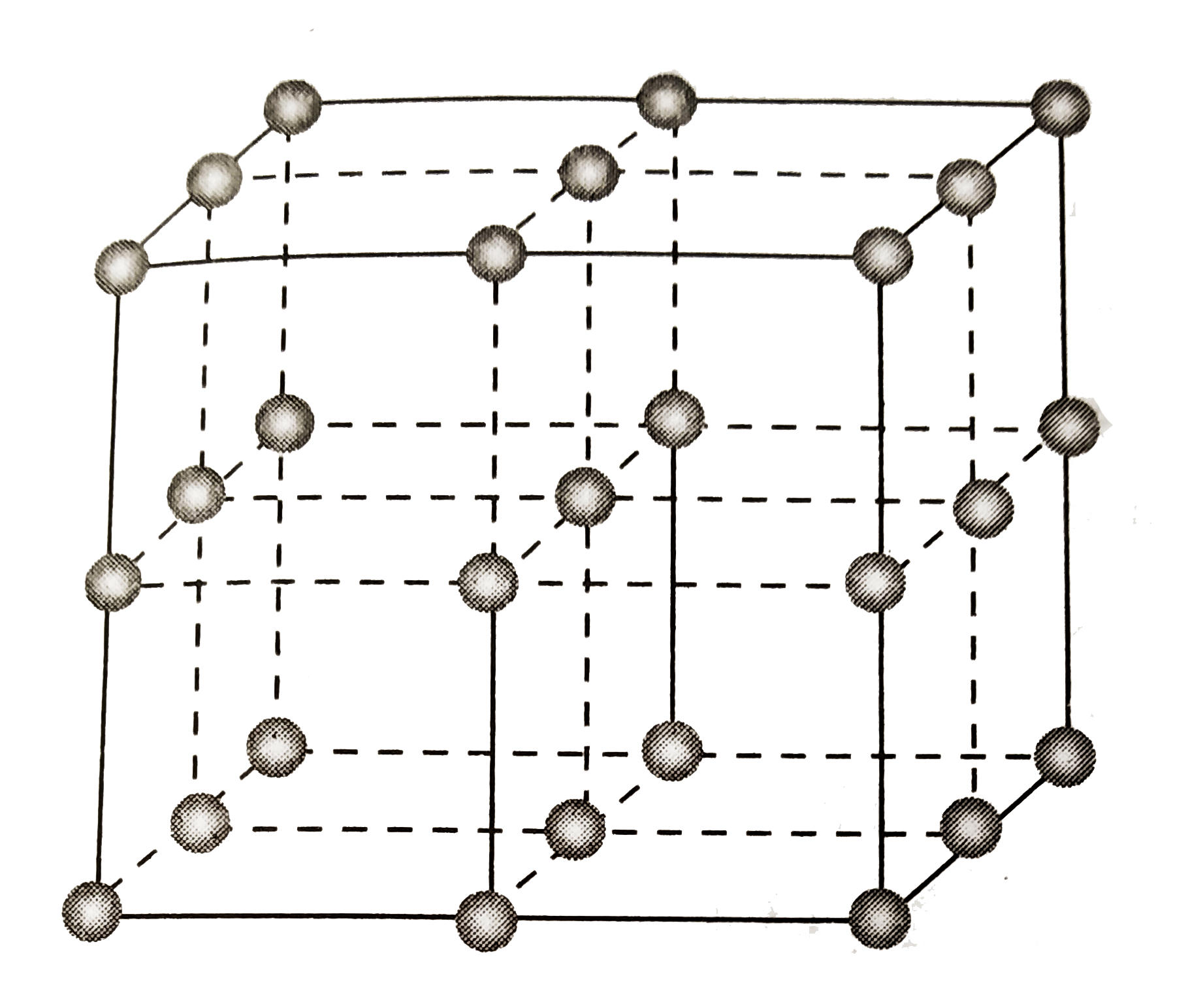
View SolutionThe following diagram shows the arrangement of lattice points with a=b=c and α=β=γ=90∘. Choose the correct options.
View SolutionThe crystal system of a compound with unit cell dimensions a=0.387,b=0.387 and c=0.504 and α=β=90∘ and γ=120∘is
View SolutionThe crystal system of a compound with unit cell dimensions a=0.350,b=0.350 and c=0.500 and α=β=90∘ and γ=120∘is
View SolutionIf ∣∣ ∣∣a+b+2cabcb+c+2abcac+a+2b∣∣ ∣∣=k(αa+βb+γc)3then(2α+β−γ)kis(α,β,γ,k∈Z+)
View SolutionIf α,β,γ are such that α+β+γ=2,α2+β2+γ2=6,α3+β3+γ3=8,thenα4+β4+γ4 is a. 18 b. 10 c. 15 d. 36
View SolutionThe crystal system of a compound with unit cell dimensions a = 0.388 , b = 0.388 and c = 0.506 nm and α=β=90∘andγ=120∘ is
View Solution
