An aqueous solution of a non-electrolyte boils at 100.52∘C . The freezing point of the solution will be
0∘C
−1.86∘C
1.86∘C
None of these
The correct Answer is:B
To find the freezing point of an aqueous solution of a non-electrolyte that boils at 100.52°C, we can follow these steps:
Step 1: Determine the elevation in boiling point
The elevation in boiling point (ΔTb) can be calculated using the formula:
ΔTb=Tb−Tb,solvent
Where:
- Tb is the boiling point of the solution (100.52°C)
- Tb,solvent is the boiling point of the pure solvent (water, which is 100°C)
Substituting the values:
ΔTb=100.52°C−100°C=0.52°C
Step 2: Use the boiling point elevation formula
The formula for boiling point elevation is:
ΔTb=i⋅Kb⋅m
Where:
- Kb is the molal elevation constant for water (approximately 0.52°C/m)
- i is the van 't Hoff factor (for non-electrolytes, i=1)
- m is the molality of the solution
Since we are considering a non-electrolyte and assuming molality m=1:
0.52°C=1⋅0.52°C/m⋅m
This confirms that the elevation in boiling point is consistent with a molality of 1.
Step 3: Set up the freezing point depression formula
The formula for freezing point depression is:
ΔTf=i⋅Kf⋅m
Where:
- Kf is the molal depression constant for water (approximately 1.86°C/m)
- i is the van 't Hoff factor (for non-electrolytes, i=1)
Using m=1:
ΔTf=1⋅1.86°C/m⋅1=1.86°C
Step 4: Calculate the freezing point of the solution
The freezing point depression (ΔTf) is defined as:
ΔTf=Tf,solvent−Tf,solution
Where:
- Tf,solvent is the freezing point of the pure solvent (water, which is 0°C)
Rearranging gives us:
Tf,solution=Tf,solvent−ΔTf
Substituting the values:
Tf,solution=0°C−1.86°C=−1.86°C
Final Answer
The freezing point of the solution is −1.86°C.
---
The elevation in boiling point (ΔTb) can be calculated using the formula:
ΔTb=Tb−Tb,solvent
Where:
- Tb is the boiling point of the solution (100.52°C)
- Tb,solvent is the boiling point of the pure solvent (water, which is 100°C)
ΔTb=100.52°C−100°C=0.52°C
The formula for boiling point elevation is:
ΔTb=i⋅Kb⋅m
Where:
- Kb is the molal elevation constant for water (approximately 0.52°C/m)
- i is the van 't Hoff factor (for non-electrolytes, i=1)
- m is the molality of the solution
0.52°C=1⋅0.52°C/m⋅m
This confirms that the elevation in boiling point is consistent with a molality of 1.
The formula for freezing point depression is:
ΔTf=i⋅Kf⋅m
Where:
- Kf is the molal depression constant for water (approximately 1.86°C/m)
- i is the van 't Hoff factor (for non-electrolytes, i=1)
ΔTf=1⋅1.86°C/m⋅1=1.86°C
The freezing point depression (ΔTf) is defined as:
ΔTf=Tf,solvent−Tf,solution
Where:
- Tf,solvent is the freezing point of the pure solvent (water, which is 0°C)
Tf,solution=Tf,solvent−ΔTf
Substituting the values:
Tf,solution=0°C−1.86°C=−1.86°C
The freezing point of the solution is −1.86°C.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUID SOLUTIONSEXERCISE - IN-CHAPTER EXERCISE -I10videos
LIQUID SOLUTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUID SOLUTIONSEXERCISE - IN-CHAPTER EXERCISE -J10videos
LIQUID SOLUTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUID SOLUTIONSEXERCISE - IN-CHAPTER EXERCISE -G9videos
LIQUID SOLUTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUID SOLUTION EXERCISE - IMPECCABLE100videos
LIQUID SOLUTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART II : CHEMISTRY (SECTION-2)10videos
MOCK TEST 1
Similar Questions
The boiling point of an aqueous solution of a non - electrolyte is 100.52∘C . Then freezing point of this solution will be [ Given : kf=1.86 K kg mol−1,kb=0.52kg mol−1 for water]
View Solution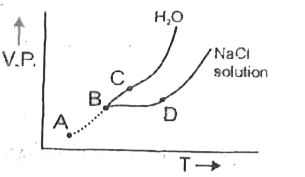
Freezing point of solution is marked asView SolutionThe boiling point of an aqueous solution of a non-volatile solute is 100.15∘C. What is the freezing point of an aqueous solution obtained by dilute the above solution with an equal volume of water. The values of Kb and Kf for water are 0.512 and 1.86∘Cmol−1:
View SolutionThe boiling point of an aqueous solution of a non-volatile solute is 100.15∘C. What is the freezing point of an aqueous solution obtained by dilute the above solution with an equal volume of water. The values of Kb and Kf for water are 0.512 and 1.86∘Cmol−1:
View SolutionThe freezing poing of an aqueous solution of a non-electrolyte is −0.14∘C. The molality of this solution is [Kf(H2O)=1.86kgmol−1]:
View SolutionAn aqueous solution of a non-volatile solute boils at 100.17∘C. At what temperature will the solution freeze? (Given: Kb=0.512 and Kf=1.86)
View Solution1.0 molal aqueous solution of an electrolyte X3Y2 is 25% ionized. The boiling point of the solution is (Kb for H2O=0.52Kkg/mol):
View SolutionOn diluting aqueous solution of weak electrolyte to 100 times
View Solution0.1 molal aqueous solution of an electrolyte AB3 is 90% ionised. The boiling point of the solution at 1 atm is (Kb(H2O)=0.52kg mol−1)
View SolutionA 1.24 M aqueous solution of KI has a density of 1.15gcm−3. What is the freezing point of the solution if the KI is completely dissociated in the solution?
View Solution

