Which of the following relations is correct?
→A+B=→C
→A+→B=C
→A+→B=→C
A+→B=→C
The correct Answer is:C
To solve the question, we need to analyze each of the given options to determine which relation is correct based on the properties of vectors and magnitudes.
1. Understanding Vectors and Magnitudes:
- Vectors are quantities that have both magnitude and direction (e.g., velocity, force).
- The magnitude of a vector is a scalar quantity that represents the size or length of the vector (e.g., speed).
2. Analyzing the Options:
- Option A: a+|b|=c
- Here, we are adding a vector a and the magnitude of vector b (which is a scalar). This operation is not valid because you cannot add a vector and a scalar directly. Hence, this option is incorrect.
- Option B: a+b=|c|
- This implies that the sum of two vectors a and b equals the magnitude of vector c. This is not a valid vector equation because the left side is a vector while the right side is a scalar. Hence, this option is incorrect.
- Option C: a+b=c
- This states that the sum of two vectors a and b results in another vector c. This is a valid vector equation, as vectors can be added together to yield another vector. Hence, this option is correct.
- Option D: |a|+b=c
- Here, we are adding the magnitude of vector a (a scalar) to vector b. This operation is not valid because you cannot add a scalar and a vector directly. Hence, this option is incorrect.
3. Conclusion:
- After analyzing all the options, we find that the only correct relation is given by Option C: a+b=c.
Final Answer:
The correct relation is Option C: a+b=c.
- Vectors are quantities that have both magnitude and direction (e.g., velocity, force).
- The magnitude of a vector is a scalar quantity that represents the size or length of the vector (e.g., speed).
- Option A: a+|b|=c
- Here, we are adding a vector a and the magnitude of vector b (which is a scalar). This operation is not valid because you cannot add a vector and a scalar directly. Hence, this option is incorrect.
- Option B: a+b=|c|
- This implies that the sum of two vectors a and b equals the magnitude of vector c. This is not a valid vector equation because the left side is a vector while the right side is a scalar. Hence, this option is incorrect.
- This states that the sum of two vectors a and b results in another vector c. This is a valid vector equation, as vectors can be added together to yield another vector. Hence, this option is correct.
- Here, we are adding the magnitude of vector a (a scalar) to vector b. This operation is not valid because you cannot add a scalar and a vector directly. Hence, this option is incorrect.
- After analyzing all the options, we find that the only correct relation is given by Option C: a+b=c.
The correct relation is Option C: a+b=c.
Similar Questions
Knowledge Check
Which of the following relation is correct?
AB=Bv×BHBB=Bv/BHCB=Bv+BHDB=√B2v+B2H
Which of the following relation is correct for kf and kb in an equibilirium process that contains equal moles of rectants and products.
View SolutionWhich of the following relation is correct with respect to first (I) and second (II) ionization enthalpies of potassium and calcium?
View SolutionWhich of the following relation is correct with respect first (I) and second (II) ionisation potential of sodium and magnesium?
View SolutionWhich of the following relation is correct for the calculation of workdone in expansion of an ideal gas by a reversible and adiabatic process.
View SolutionFor two particles A and B, curves are plotted √V against de-Broglie wavelengths, where V is the potential on the particles. Which of the following relation is correct about the mass of particles?
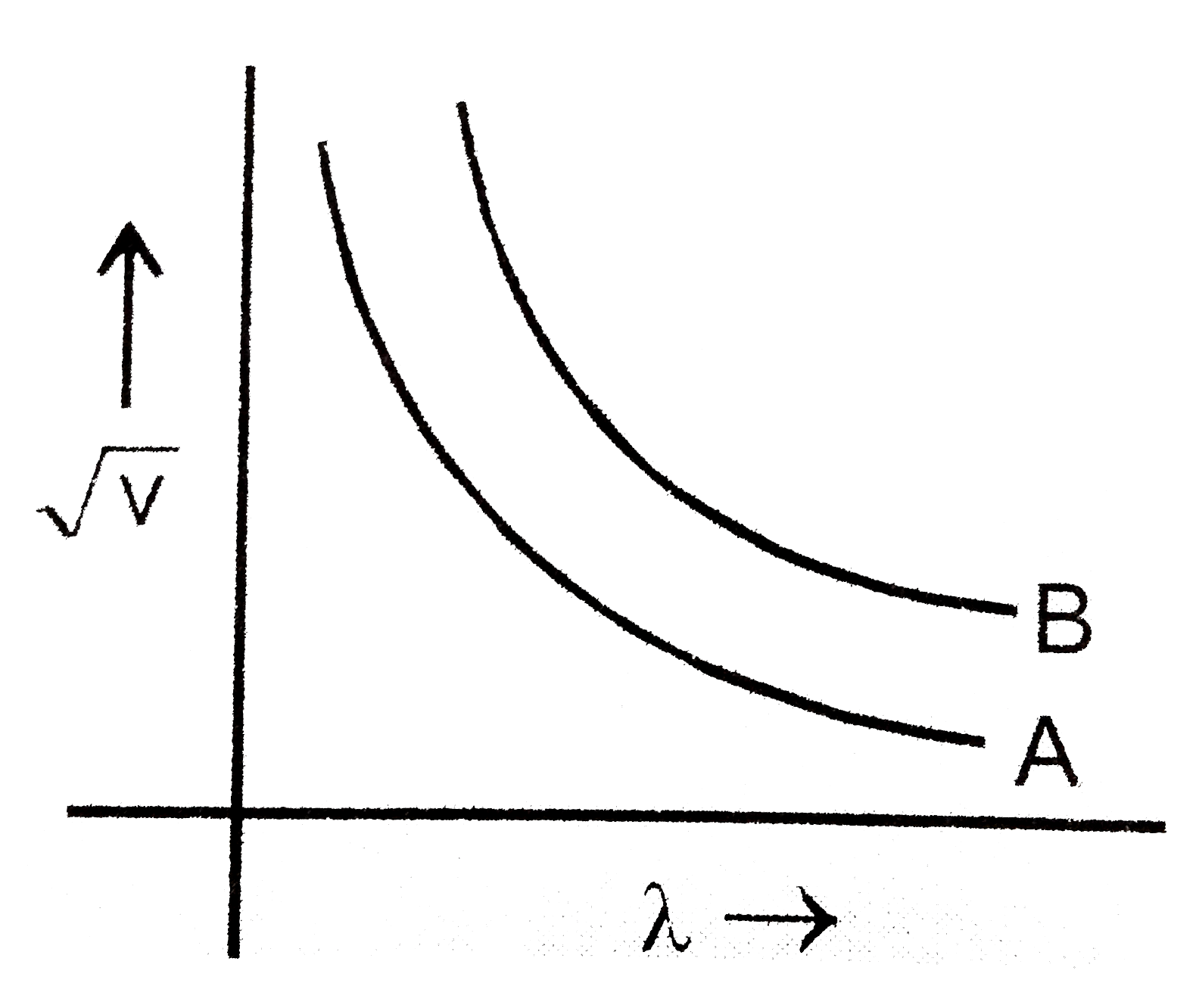
View SolutionThe initial velocity of a particle is x ms−1 (at t=0) and acceleration a is function for time, given by, a= 6t. Which of the following relation is correct for final velocity y after time t?
View SolutionThe enthalpies of neutralization to two weak acids HA and HB
with NaOH are −10.1 and −11.8 Kcal/g. eq respectively.
Which of the following relation is correct regarding acidic
strengths of HA and HB :−
View Solution
