Suppose →a is a vector of magnitude 4.5 unit due north. What is the vector −4→a?
To solve the problem, we need to find the vector −4→A given that →A is a vector of magnitude 4.5 units directed due north.
1. Identify the given vector:
We have a vector →A with a magnitude of 4.5 units directed due north. This can be represented as:
→A=4.5units(north)
2. Understand the operation:
We need to find −4→A. This means we will multiply the vector →A by −4.
3. Calculate the magnitude of −4→A:
When multiplying a vector by a scalar, the magnitude of the new vector is the absolute value of the scalar multiplied by the magnitude of the original vector. Thus:
Magnitude of −4→A=|−4|×|→A|=4×4.5=18units
4. Determine the direction of −4→A:
Since we are multiplying by a negative scalar (-4), the direction of the vector will be reversed. The original vector →A is directed due north, so −4→A will be directed due south.
5. Write the final result:
Therefore, the vector −4→A can be expressed as:
−4→A=18units(south)
Final Answer:
−4→A=18units(south)
We have a vector →A with a magnitude of 4.5 units directed due north. This can be represented as:
→A=4.5units(north)
We need to find −4→A. This means we will multiply the vector →A by −4.
When multiplying a vector by a scalar, the magnitude of the new vector is the absolute value of the scalar multiplied by the magnitude of the original vector. Thus:
Magnitude of −4→A=|−4|×|→A|=4×4.5=18units
Since we are multiplying by a negative scalar (-4), the direction of the vector will be reversed. The original vector →A is directed due north, so −4→A will be directed due south.
Therefore, the vector −4→A can be expressed as:
−4→A=18units(south)
−4→A=18units(south)
Similar Questions
Suppose →a is a vector of magnitude 4.5 unit due north. What is the vector 3→a
View SolutionSuppose →a is a vector of magnitude 4.5 unit due north. What is the vector a. 3→a,b−4→a?
View SolutionSuppose →a is a vector of magnitude 4.5 unit due north. What is the vector (a) 3→a (b) −4→a?
View Solution→A is a vector of magnitude 2.7 units due east . What is the magnitude and direction of vector 4 →A ?
View SolutionFind a vector of magnitude 5 units, and parallel to the resultant of the vectors
→a=2ˆi+3ˆj−ˆkand→b=ˆi−2ˆj+ˆk.View SolutionFind a vector of magnitude 9 units and perpendicular to the vectors
→a=4ˆi−ˆj+ˆkand→b=−2ˆi+ˆj−2ˆk.View SolutionFind a vector whose magnitude is 3 units and which is perpendicular to the vectors →aand→b where →a=3ˆi+ˆj−4ˆkand→b=6ˆi+ˆj−2ˆk
View SolutionVector →A of magnitude 4 units is directed along the positive x-axis. Another vector →B of magnitude 3 units lies in the x-y plane and is directed along 30∘ with the positive x-axis is as shown in figure. The magnitude of dot product →A.→B is:
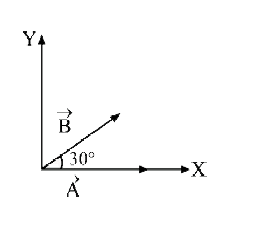 View Solution
View SolutionIf →a,→band→c are three vectors of which every pair is non colinear. If the vector →a+→band→b+→c are collinear with the vector →c and →a respectively then which one of the following is correct? (A) →a+→b+→c is a nul vector (B) →a+→b+→c is a unit vector (C) →a+→b+→c is a vector of magnitude 2 units (D) →a+→b+→c is a vector of magnitude 3 units
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View Solution

