A current I ampere flows along an infinitely long straight thin walled tube, then the magnetic induction at any point inside the tube is .
Infinite
Zero
μ04π.2IR
2IR
The correct Answer is:2
To find the magnetic induction at any point inside an infinitely long straight thin-walled tube carrying a current I, we can follow these steps:
1. Understand the Geometry:
- Visualize the thin-walled tube as a cylindrical shell with a circular cross-section. The current I flows uniformly along the circumference of the tube.
2. Identify the Magnetic Field Inside the Tube:
- We need to determine the magnetic field at a point inside the tube. Since the tube is hollow, there is no current flowing through the area inside the tube.
3. Apply Ampère's Circuital Law:
- According to Ampère's Circuital Law, the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current Ienc enclosed by that loop:
∮B⋅dl=μ0Ienc
4. Choose an Amperian Loop:
- Consider a circular Amperian loop of radius r inside the tube. Since the tube is hollow, the current enclosed by this loop is zero because all the current flows along the circumference of the tube.
5. Evaluate the Integral:
- Since there is no current enclosed by the Amperian loop, we have:
Ienc=0
- Therefore, applying Ampère's law gives:
∮B⋅dl=μ0⋅0=0
6. Conclude the Magnetic Field Inside the Tube:
- Since the line integral of the magnetic field around the loop is zero, it implies that the magnetic field B inside the tube must also be zero:
B=0
Final Answer:
The magnetic induction at any point inside the tube is B=0.
- Visualize the thin-walled tube as a cylindrical shell with a circular cross-section. The current I flows uniformly along the circumference of the tube.
- We need to determine the magnetic field at a point inside the tube. Since the tube is hollow, there is no current flowing through the area inside the tube.
- According to Ampère's Circuital Law, the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current Ienc enclosed by that loop:
∮B⋅dl=μ0Ienc
- Consider a circular Amperian loop of radius r inside the tube. Since the tube is hollow, the current enclosed by this loop is zero because all the current flows along the circumference of the tube.
- Since there is no current enclosed by the Amperian loop, we have:
Ienc=0
- Therefore, applying Ampère's law gives:
∮B⋅dl=μ0⋅0=0
- Since the line integral of the magnetic field around the loop is zero, it implies that the magnetic field B inside the tube must also be zero:
B=0
The magnetic induction at any point inside the tube is B=0.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 4
4 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 5
5 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 2
2 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
A current I flows along an inflinitely long straight thin walled tube. The magnetic induction at a point inside the tube at a distance r from its wall is
View SolutionA current i flows along the length of an infinitely long, straight, thin-walled pipe. Then,
(a) the magnetic field at all points inside the pipe is the same, but not zero
(b) the magnetic field at any point inside the pipe is zero
(c) the magnetic field is zero only on the axis of the pipe
(d) the magnetic field is different at different points inside the pipe
View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View SolutionA current of 1/(4π) ampere is flowing in a long straight conductor. The line integral of magnetic induction around a closed path enclosing the current carrying conductor is
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View SolutionA magnet is dropped down an infinitely long vertical copper tube
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionThe current I ampere is flowing in an equilateral triangle of side a the magnetic field induction at the centroid will be
View SolutionIn the diagram shown, I1,I2 are the magnitudes of current in the squre loop and infinite long straight conductor respectively. If the net magnetic field at the centre of the loop is zero, then the relation between I1andI2 is
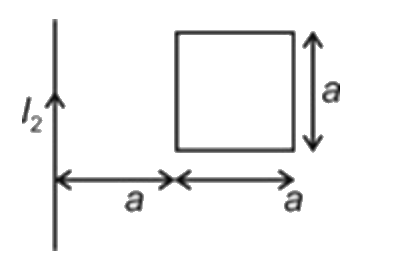
View Solution
