Find the angle through which a magnet is to be rotated from rest position when it is suspended in a magnetic field so that it experiences half of the maximum couple
60∘
30∘
45∘
90∘
The correct Answer is:2
To solve the problem of finding the angle through which a magnet must be rotated from its rest position to experience half of the maximum couple in a magnetic field, we can follow these steps:
1. Understanding Torque in a Magnetic Field:
The torque (τ) experienced by a magnetic dipole in a magnetic field is given by the formula:
τ=M×B
where M is the magnetic dipole moment and B is the magnetic field.
2. Expressing Torque in Terms of Angle:
The magnitude of torque can also be expressed as:
τ=MBsinθ
where θ is the angle between the magnetic moment and the magnetic field.
3. Finding Maximum Torque:
The maximum torque (τmax) occurs when sinθ=1 (i.e., θ=90∘):
τmax=MB
4. Setting Up the Equation for Half Maximum Torque:
We need to find the angle θ when the torque is half of the maximum torque:
τ=τmax2=MB2
5. Substituting into the Torque Equation:
Substitute τ into the torque equation:
MB2=MBsinθ
6. Simplifying the Equation:
Cancel MB from both sides (assuming M and B are not zero):
12=sinθ
7. Finding the Angle θ:
To find θ, take the inverse sine:
θ=sin−1(12)
This gives:
θ=30∘
8. Calculating the Rotation from the Rest Position:
The rest position of the magnet is at 0∘. To find the angle through which the magnet must be rotated:
Rotation=90∘−30∘=60∘
Final Answer:
The angle through which the magnet is to be rotated from the rest position to experience half of the maximum couple is:
Rotation=60∘
The torque (τ) experienced by a magnetic dipole in a magnetic field is given by the formula:
τ=M×B
where M is the magnetic dipole moment and B is the magnetic field.
The magnitude of torque can also be expressed as:
τ=MBsinθ
where θ is the angle between the magnetic moment and the magnetic field.
The maximum torque (τmax) occurs when sinθ=1 (i.e., θ=90∘):
τmax=MB
We need to find the angle θ when the torque is half of the maximum torque:
τ=τmax2=MB2
Substitute τ into the torque equation:
MB2=MBsinθ
Cancel MB from both sides (assuming M and B are not zero):
12=sinθ
To find θ, take the inverse sine:
θ=sin−1(12)
This gives:
θ=30∘
The rest position of the magnet is at 0∘. To find the angle through which the magnet must be rotated:
Rotation=90∘−30∘=60∘
The angle through which the magnet is to be rotated from the rest position to experience half of the maximum couple is:
Rotation=60∘
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 12
4 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 13
3 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE10
1 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
A wire of length l is formed into a circular loop of one turn only and is suspended in a magnetic field B. When a current i is passed through the loop, the maximum torque experienced by it is
View SolutionWhen passing through a magnetic field the largest degflection is experienced by
View SolutionA bar magnet of magnetic moment 2.0 A−m2 is free to rotate about a vertical axis through its centre. The magnet is released from rest from the east west position. Find the kinetic energy of the magnet as it takes the north south position. The horizontal component of the earth's magnetic field as B=25μT. Earth's magnetic field is from south to north.
View SolutionIf a magnet is suspended an angle 30∘ to the magnetic field at any point on eath. Near the north pole.
View SolutionA steel wire can withstand a load up to 2940N. A load of 150kg is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load pass through the position of equilibrium, is
View SolutionA bar magnet of magnetic moment 2.0Am2 is free to rotate about a vertical axis through its centre. The magnet is released from rest from the east-west position. Find the kinetic energy of the magnet as it takes the north-south position. The horizontal component of the earth's magnetic field is B=25μT.
View SolutionA: A magnetic dipole experiences maximum torque when it is placed normal to the magnetic field.
R: The minimum potential energy of magnetic dipole is zero.
View SolutionSTATEMENT-1 : When a soft iron bar is suspended freely in earth's magnet field it does not show directional property .
and
STATEMENT-2 : When soft iron is placed in magnetic field it does not experience force .
View SolutionA magnet of magnetic moment M is rotated through 360∘ in a magnetic field H, the work done will be
View SolutionAn angle aob made of a conducting wire moves along its bisector through a magnetic field B as suggested by figure. Find the emf induced between the two free ends if the magnetic field is perpendicular ot the plane of the angle.

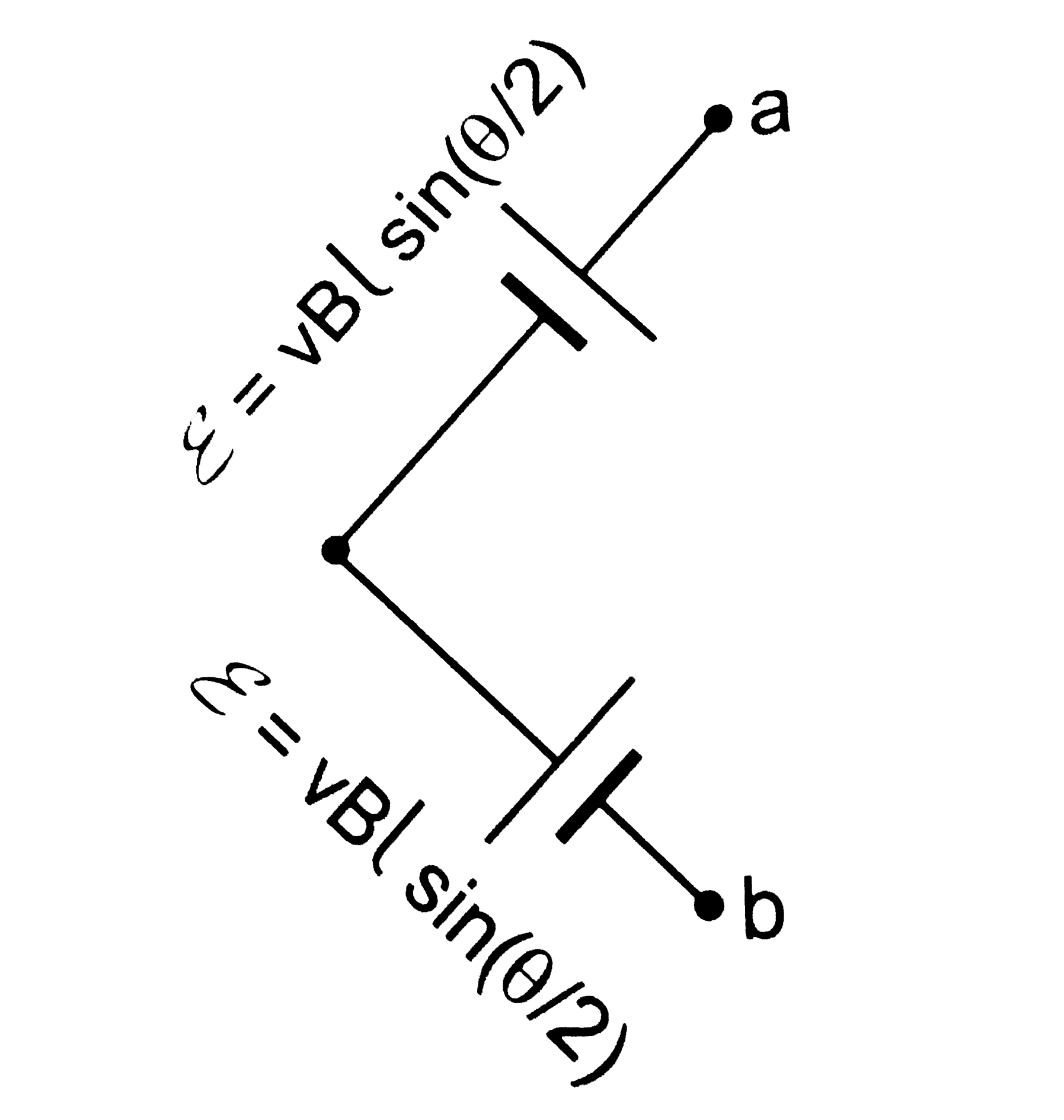
View Solution
