A series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depends upon
Land R only
E And L only
E and R only
L, R and E only
The correct Answer is:C
To solve the problem, we need to determine the final value of the current in a series combination of an inductor (L) and a resistor (R) connected to a battery with an electromotive force (emf) E.
1. Understand the Circuit Configuration:
- We have a series circuit consisting of an inductor (L) and a resistor (R) connected to a battery of emf E. The internal resistance of the battery is negligible.
2. Apply Kirchhoff's Voltage Law:
- According to Kirchhoff's law, the sum of the potential differences in a closed loop must equal zero. For our circuit, we can write:
E−iR−Ldidt=0
where i is the current flowing through the circuit.
3. Analyze the Current Over Time:
- The current i in the circuit will not be constant initially; it will increase from zero to a maximum value as the inductor opposes the change in current. The equation governing the growth of current is given by:
i(t)=ER(1−e−RLt)
- Here, e−RLt represents the exponential decay factor that approaches zero as time t approaches infinity.
4. Determine the Final Current:
- As time approaches infinity (t→∞), the exponential term e−RLt approaches zero. Therefore, the final steady-state current i becomes:
i=ER
5. Conclusion:
- The final value of the current depends only on the emf E and the resistance R. The inductance L does not affect the final steady-state current; it only affects how quickly the current reaches that final value.
Final Answer:
The final value of current depends upon E and R only.
Options:
- E and L only
- E and R only (Correct)
- L and R only
- L, R, and E only
- We have a series circuit consisting of an inductor (L) and a resistor (R) connected to a battery of emf E. The internal resistance of the battery is negligible.
- According to Kirchhoff's law, the sum of the potential differences in a closed loop must equal zero. For our circuit, we can write:
E−iR−Ldidt=0
where i is the current flowing through the circuit.
- The current i in the circuit will not be constant initially; it will increase from zero to a maximum value as the inductor opposes the change in current. The equation governing the growth of current is given by:
i(t)=ER(1−e−RLt)
- Here, e−RLt represents the exponential decay factor that approaches zero as time t approaches infinity.
- As time approaches infinity (t→∞), the exponential term e−RLt approaches zero. Therefore, the final steady-state current i becomes:
i=ER
- The final value of the current depends only on the emf E and the resistance R. The inductance L does not affect the final steady-state current; it only affects how quickly the current reaches that final value.
The final value of current depends upon E and R only.
- E and L only
- E and R only (Correct)
- L and R only
- L, R, and E only
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 3
4 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 4
5 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 1
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
(a) Three resistors 2Ω,4Ωand5Ω are combined in parallel. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
View Solution(a) Three resistors 1Ω,2Ω and 3Ω are combined in series. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
View Solution
Knowledge Check
Three resistances 2Ω,4Ω,5Ω are combined in series and this combination is connected to a battery of 12 V emf and negligible internal resistance. The potential drop across these resistances are
A(5,45,4.36,2.18)VB(2,18,5.45,4.36)VC(4.36,2.18,5.45)VD(2.18,4.36,5.45)VThree resistors 2Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 20V and negligible internal Resistance. The total current drawn from the battery is
A10AB15AC19AD23AThree resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4,3,2.4B8,7,3,4C2,5,1,8D5,5,8,2
Two resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionA 10 m along uniform metallic wire having a resistance of 20Ω is used as a potentiometer wire. This wire is connected in series with another resistance of 480Ω and a battery of emf 5 V having negligible internal resistance . If an unknown emf e is balanced across 6 m of the potentiometer wire. Calculate :
(i) The potential gradient across the potentiometer wire.
(ii) the value of the unknown emf e.
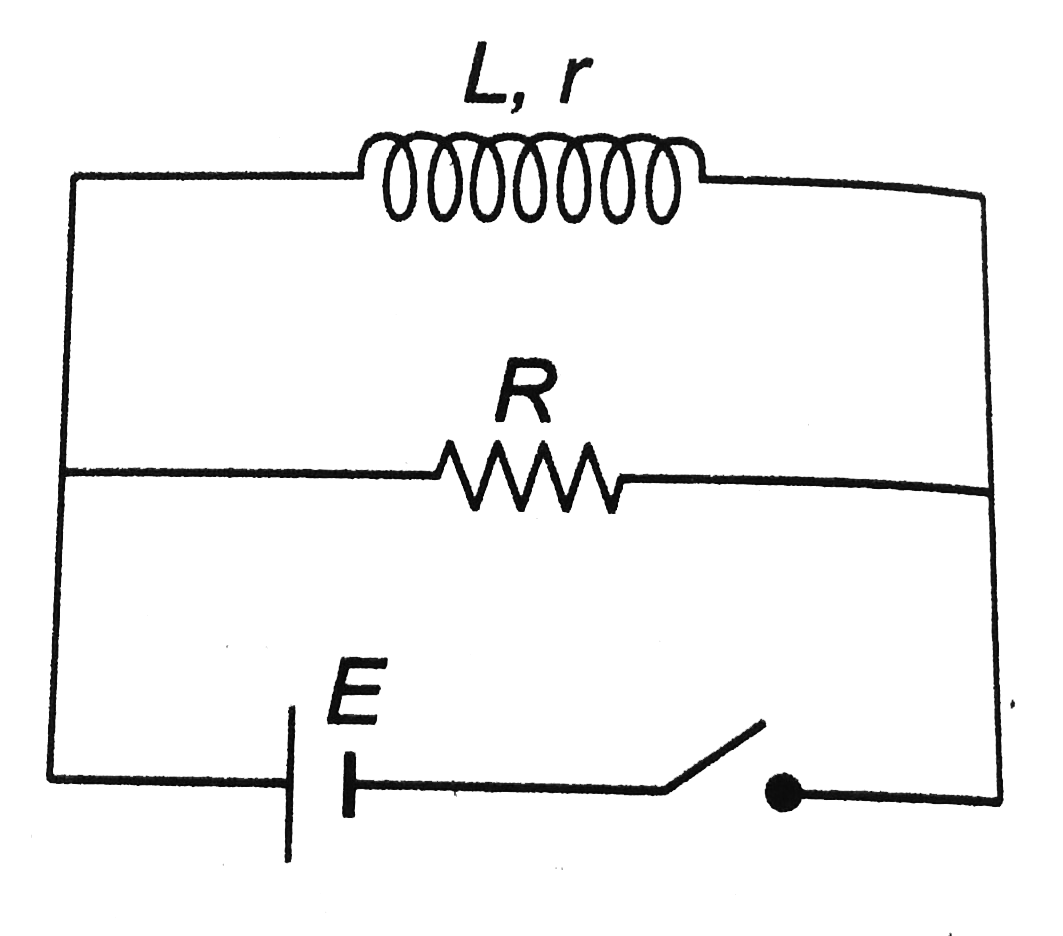
View SolutionA solenoid of inductance L with resistance r is connected in parallel to a resistance R. A battery of emf E and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time t=0, switch S is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
View SolutionA set of 'n' equal resistor, of value of 'R' each are connected in series to a battery of emf 'E' and internal resistance 'R'. The current drawn is I. Now, the 'n' resistors are connected in parallel to the same battery. Then the current drawn from battery becomes 10.1. The value of 'n' is
View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
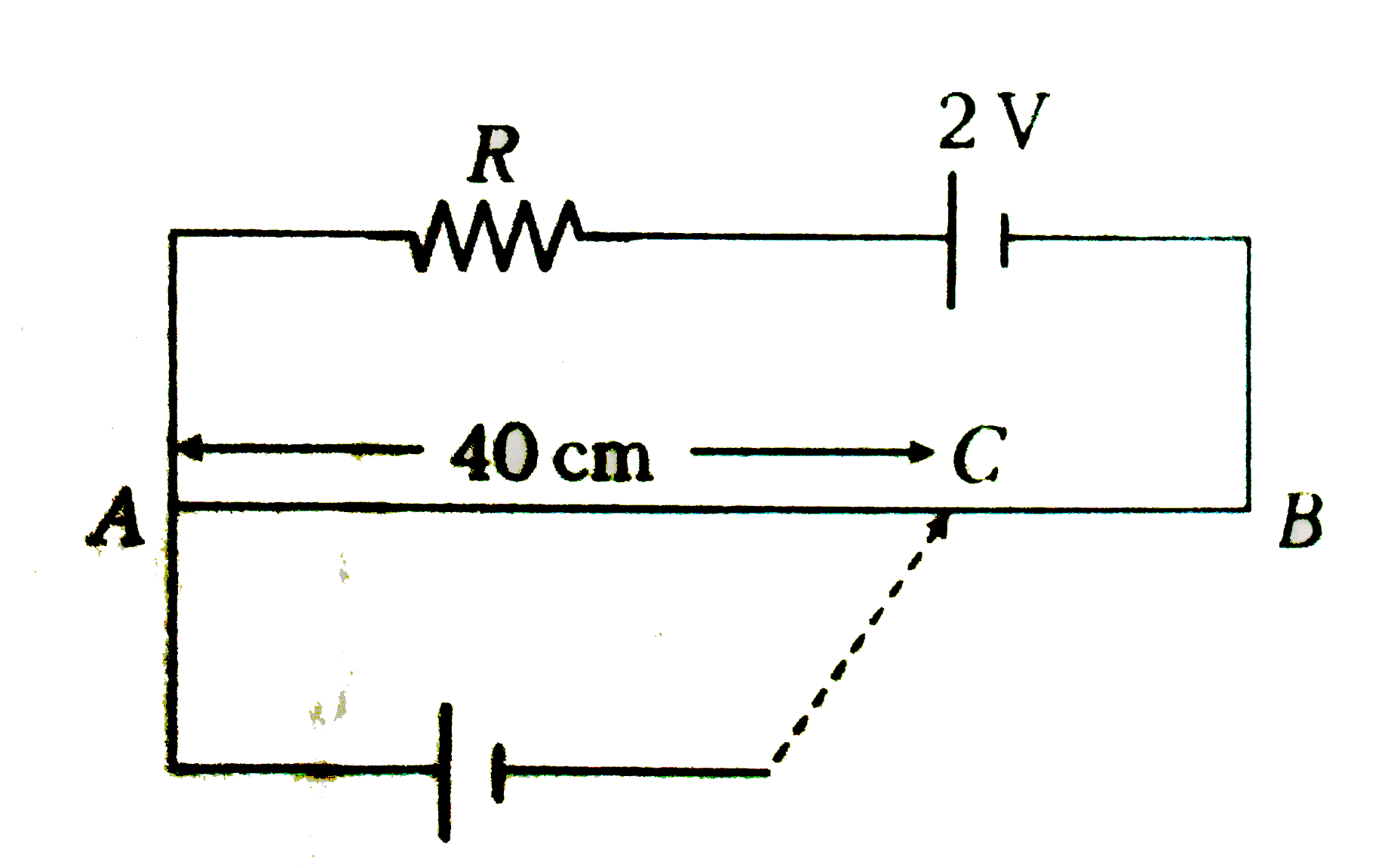
View Solution
