The average power dissipated in a pure capacitance AC circuit is
CV
Zero
The correct Answer is:B
Step by step video & image solution for The average power dissipated in a pure capacitance AC circuit is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-E
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
The average power dissipation in a pure capacitance in AC circuit is
View SolutionThe average power is dissipated in a pure inductor is
View SolutionThe average power dissipated in a pure inductor L carrying an alternating current of rms value I is .
View SolutionPower dissipated in pure inductance will be-
View SolutionIn a series LCR circuit, an alternating emf (V) and current (I) are given by the equation V=V0sinωt,I=I0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
View SolutionThe average power dissipated in AC circuit is 2W. If a current flowing throuh a circuit is 2A, impedance is 1Ω, then what is the power factor of the circuit?
View SolutionIn a purely resistive AC circuit,
View SolutionThe power dissipated in the adjacent circuit is -
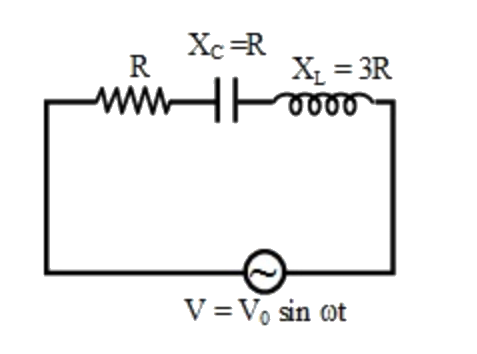
View SolutionA capacitor of capacitance 2 mF and resistor of resistance 12 Ω are connected in series with voltage source V=(195√2(V))[sin(100rads)t] - The average power dissipated in the circuit will be
View SolutionThe power dissipated in the resistance R, in the circuit as shown in the figure, is maximum if R is equal to
View Solution
