Question

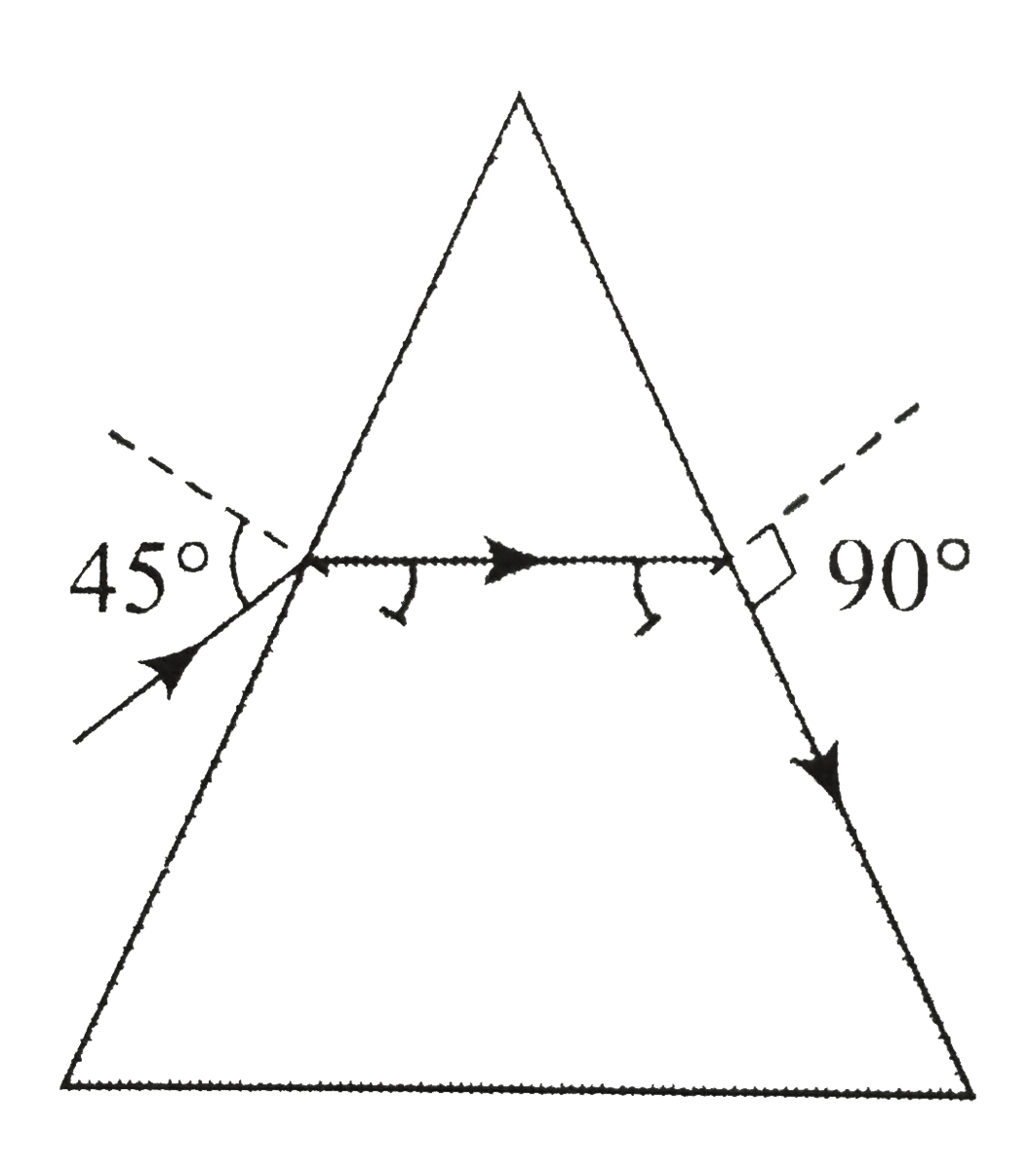
The light ray is incidence at angle of ${60}^{\circ }$ on a prism of angle ${45}^{\circ }$ . When the light ray falls on the other surface at ${90}^{\circ }$ , the refractive index of the material of prism$\mu$ and the angle of devaition $\delta$ are given by

Options

A. (a)`mu=sqrt(2),delta=30^@`
B. (b)`mu=1.5,delta=15^@`
C. (c)`mu=sqrt(3)/2,delta=30^@`
D. (d)`mu=sqrt(3/2),delta=15^@`

Answer

4

Explanation

To solve the problem, we need to determine the refractive index (μ) of the prism and the angle of deviation (δ) when a light ray strikes a prism with an angle of 45° at an incidence angle of 60° and exits at 90°.

1. Draw the Prism:
- Draw a prism and label the vertices as A, B, and C. The angle at the prism (A) is given as 45°.

2. Identify the Angles:
- The angle of incidence (i) is given as 60°.
- The light ray strikes the surface at an angle of 90° upon exiting.

3. Apply Snell's Law at the First Surface (AB):
- According to Snell's law, we have:
\( \mu = \frac{\sin(i)}{\sin(r_1)} \)
- Here, \(i = 60°\) and \(r_1\) is the angle of refraction at the first surface.

4. Determine the Angle of Refraction (r1):
- The angle of the prism (A) is given as 45°. Therefore, we can express the relationship between the angles as:
\( A = r_1 + r_2 \)
- Since the light ray exits at 90°, we have \(r_2 = 0°\) (the angle of refraction at surface BC is 0°). Thus:
\( r_1 + 0° = 45° \implies r_1 = 45° \)

5. Calculate the Refractive Index (μ):
- Substitute the known values into Snell's law:
\( \mu = \frac{\sin(60°)}{\sin(45°)} \)
- We know:
\( \sin(60°) = \frac{\sqrt{3}}{2}, \quad \sin(45°) = \frac{\sqrt{2}}{2} \)
- Therefore:
\( \mu = \frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}} = \frac{\sqrt{3}}{\sqrt{2}} = \sqrt{\frac{3}{2}} \)

6. Calculate the Angle of Deviation (δ):
- The angle of deviation is given by:
\( \delta = \mu - 1 \cdot A \)
- Substitute the values:
\( \delta = \left(\sqrt{\frac{3}{2}} - 1\right) \cdot 45° \)
- Calculate the deviation:
\( \delta = \left(\sqrt{\frac{3}{2}} - 1\right) \cdot 45° \)
- Approximating \(\sqrt{\frac{3}{2}} \approx 1.2247\):
\( \delta \approx (1.2247 - 1) \cdot 45° \approx 0.2247 \cdot 45° \approx 10.1° \)
- Rounding gives approximately \(15°\).

7. Final Results:
- The refractive index of the prism is \(\sqrt{\frac{3}{2}}\).
- The angle of deviation is approximately \(15°\).