In the reaction Np23993→Pu23994+(?), the missing particle is
Proton
Positron
Electron
Neutron
The correct Answer is:C
To solve the reaction Np23993→Pu23994+(?), we need to identify the missing particle in this nuclear reaction.
1. Identify the Reactants and Products:
- The reactant is Neptunium (Np) with atomic number 93 and mass number 239.
- The product is Plutonium (Pu) with atomic number 94 and mass number 239.
2. Analyze the Change in Atomic Number:
- The atomic number of Neptunium (Np) is 93, and it changes to Plutonium (Pu) which has an atomic number of 94.
- This indicates that the atomic number has increased by 1.
3. Analyze the Change in Mass Number:
- The mass number of both Neptunium (Np) and Plutonium (Pu) is 239.
- This indicates that the mass number remains unchanged during this reaction.
4. Determine the Type of Decay:
- Since the atomic number increases by 1 while the mass number remains the same, this reaction is indicative of beta decay.
- In beta decay, a neutron in the nucleus is converted into a proton, and a beta particle (which is an electron) is emitted.
5. Identify the Missing Particle:
- In beta decay, the emitted particle is a beta particle, which can be represented as β− or an electron e−.
- Therefore, the missing particle in the reaction is a beta particle.
Final Reaction:
The complete reaction can be written as:
Np23993→Pu23994+β−
Conclusion:
The missing particle in the reaction is a beta particle (electron).
---
- The reactant is Neptunium (Np) with atomic number 93 and mass number 239.
- The product is Plutonium (Pu) with atomic number 94 and mass number 239.
- The atomic number of Neptunium (Np) is 93, and it changes to Plutonium (Pu) which has an atomic number of 94.
- This indicates that the atomic number has increased by 1.
- The mass number of both Neptunium (Np) and Plutonium (Pu) is 239.
- This indicates that the mass number remains unchanged during this reaction.
- Since the atomic number increases by 1 while the mass number remains the same, this reaction is indicative of beta decay.
- In beta decay, a neutron in the nucleus is converted into a proton, and a beta particle (which is an electron) is emitted.
- In beta decay, the emitted particle is a beta particle, which can be represented as β− or an electron e−.
- Therefore, the missing particle in the reaction is a beta particle.
The complete reaction can be written as:
Np23993→Pu23994+β−
The missing particle in the reaction is a beta particle (electron).
Similar Questions
In the reaction Li63+(?)→He42+H31. The missing particle is:
View SolutionIn the nuclear reaction U23892→Pb20682, the number of alpha and beta particles decayed are:
View Solution.^(239)Pu.94 is undergoing α−decay according to the equation .23994Pu→(.23597U)+.42He . The energy released in the process is mostly kinetic energy of the α-particle. However, a part of the energy is released as γ rays. What is the speed of the emiited α-particle if the γ rays radiated out have energy of 0.90MeV? Given: Mass of .23994Pu=239.05122u, mass of (.23597U)=235.04299u and mass of .41He=4.002602u(1u=931MeV).
View SolutionPu239 is an artificial fissile material.
View SolutionThe compound unstabel nucleus .23692U often decays in accordance with the following reaction
.23692U→.14054Xe+.9438Sr + other particles
During the reaction, the uranium nucleus ''fissions'' (splits) into the two smaller nuceli have higher nuclear binding energy per nucleon (although the lighter nuclei have lower total nuclear binding energies, because they contain fewer nucleons).
Inside a nucleus, the nucleons (protonsa and neutrons)attract each other with a ''strong nuclear'' force. All neutrons exert approxiamtely the same strong nuclear force on each other. This force holds the nuclear are very close together at intranuclear distances.
Which of the following graphs might represent the relationship between atomic number (i.e., ''atomic weight'') and the total binding energy of the nucleus, for nuclei heavier than .9438Sr ?
View SolutionIn the fission of .23994Pu by a thermal neutron, two fission fragmnets of equal masses and sizes are produced and four neutrosn are emitted. Find the force between the two fission fragments at the moment they are produced.
Given : R0=1.1 fermi.
View SolutionFind the kinetic energy of the α - particle emitted in the decay ^238Pu→234U+α. The atomic masses needed are as following:
^238Pu238.04955u
^234U234.04095u
^4He4.002603u.
Neglect any recoil of the residual nucleus.
View SolutionA fission reaction is given by _(92)236U→14054Xe+9438St+x+y , where x and y are two particle Consider _(92)236U to be at rest , the kinetic energies of the products are deneted by kxeKstKx(2MeV)andKy(2MeV) repectively . Let the binding energy per nucleus of _(92)236U,14054Xeand9438Stbe7.5MeV,8.4MeVand8.5MeV, respectively Considering different conservation laws, the correct option (s) is (are)
View SolutionThe compound unstabel nucleus .23692U often decays in accordance with the following reaction
_(92)236U→.14054Xe+9438Sr+ other particles
During the reaction, the uranium nucleus ''fissions'' (splits) into the two smaller nuceli have higher nuclear binding energy per nucleon (although the lighter nuclei have lower total nuclear binding energies, because they contain fewer nucleons).
Inside a nucleus, the nucleons (protonsa and neutrons)attract each other with a ''strong nuclear'' force. All neutrons exert approxiamtely the same strong nuclear force on each other. This force holds the nuclear are very close together at intranuclear distances.
In the nuclear reaction presented above, the ''other particles'' might be .
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
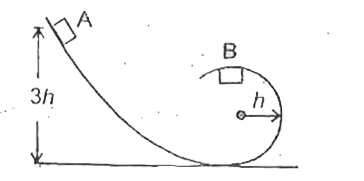
View Solution