After losing a number of αandbrta-particles, U23892 changed to Pb20682. The total number of particles lost in this process is
14
5
8
32
The correct Answer is:A
To solve the problem of how many alpha and beta particles are lost when Uranium-238 (U-238) transforms into Lead-206 (Pb-206), we can follow these steps:
Step 1: Understand the Reaction
Uranium-238 has an atomic number of 92 and a mass number of 238. It transforms into Lead-206, which has an atomic number of 82 and a mass number of 206. We need to find out how many alpha (α) and beta (β) particles are emitted during this transformation.
Step 2: Define Variables
Let:
- X = number of alpha particles emitted
- Y = number of beta particles emitted
Step 3: Conservation of Mass Number
The mass number before the reaction must equal the mass number after the reaction. The mass number of alpha particles is 4, and beta particles have a mass number of 0. Therefore, we can set up the equation:
238=206+4X+0Y
This simplifies to:
4X=238−206
4X=32
X=324=8
So, the number of alpha particles emitted is X=8.
Step 4: Conservation of Atomic Number
Next, we apply the conservation of atomic number. The atomic number of alpha particles is 2, and the atomic number of beta particles is -1. Therefore, we can set up the equation:
92=82+2X−Y
Substituting X=8:
92=82+2(8)−Y
92=82+16−Y
92=98−Y
Y=98−92=6
So, the number of beta particles emitted is Y=6.
Step 5: Total Particles Lost
Now, we can find the total number of particles lost:
Total particles lost=X+Y=8+6=14
Conclusion
The total number of particles lost in the process is 14.
---
Uranium-238 has an atomic number of 92 and a mass number of 238. It transforms into Lead-206, which has an atomic number of 82 and a mass number of 206. We need to find out how many alpha (α) and beta (β) particles are emitted during this transformation.
Let:
- X = number of alpha particles emitted
- Y = number of beta particles emitted
The mass number before the reaction must equal the mass number after the reaction. The mass number of alpha particles is 4, and beta particles have a mass number of 0. Therefore, we can set up the equation:
4X=32
X=324=8
Next, we apply the conservation of atomic number. The atomic number of alpha particles is 2, and the atomic number of beta particles is -1. Therefore, we can set up the equation:
92=82+16−Y
92=98−Y
Y=98−92=6
Now, we can find the total number of particles lost:
The total number of particles lost in the process is 14.
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph of the total number of α-particles scattered at different angles in a given interval of time for α- particles scattering in the geiger- marsden experiment is given by
A B
B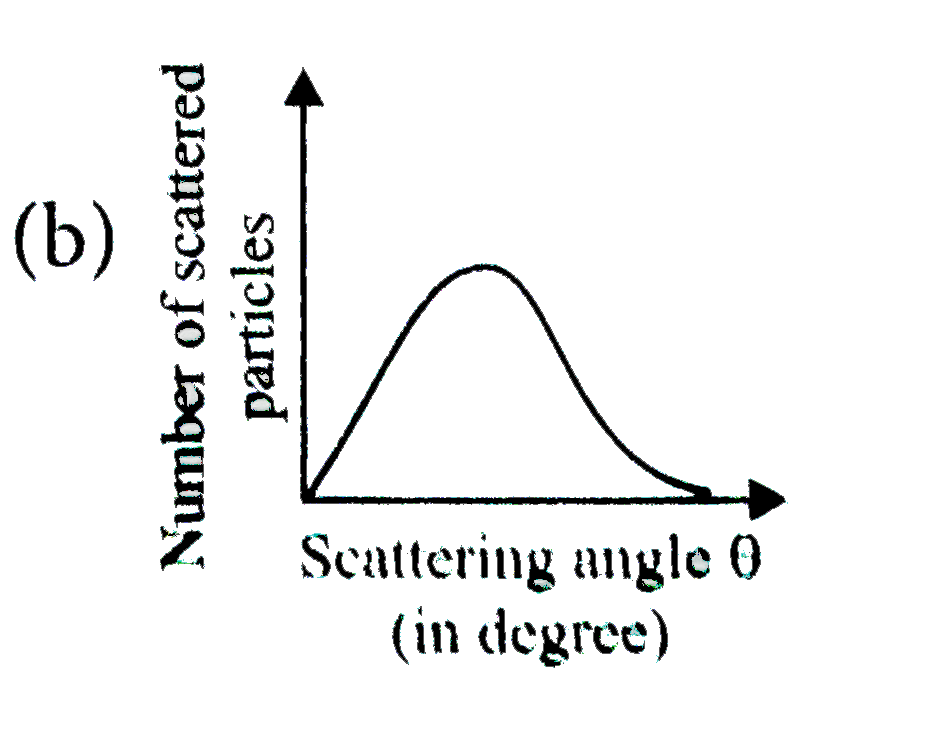 C
C D
D
In the Rutherford scattering experiment the number of α particles scattered at anangle θ=60∘ is 12 per min. The number of α particles per minute when scattered at an angle of 90∘ are
View SolutionAtomic weight of Th is 232 and its atomic number is 90. The number of α- and β-particles which be lost so that an isotope of lead (atomic weight 208 and atomic number 82) is produced is
View SolutionAc23189givesPb20782 after emission of some αandβ-particles. The number of such and -particles are respectively:
View SolutionAfter the emission of α-particle from the atom X23892, the number of neutrons in the atom will be
View Solution.23592U decays with emission of α and β- particles to form ultimately .20782Pb. How many α and β-particles are emitted per atom of Pb produced?
View SolutionA uranium nucleus U−238 of atomic number92 emits two α- particles and two β-particles and trasnforms into a thorium nucleus. What is the mass number and atomic number of the thorium nucleus so produced?
View SolutionHow may α− and β− particles will be emitted when .90Th232 changes into .82Pb208?
View Solution

