The energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1. Calculate Equilibrium constant Ka for the reaction at 300 K
To calculate the equilibrium constant Ka for the reaction A⇌B at 300 K given that the energy change (ΔH) is −33.0kJ mol−1, we can follow these steps:
Step 1: Understand the relationship between ΔH and activation energies
The change in enthalpy (ΔH) for the reaction is related to the activation energies of the forward (Ef) and backward (Eb) reactions by the equation:
ΔH=Ef−Eb
Given that ΔH=−33.0kJ mol−1, we can express this as:
−33.0=Ef−Eb
Step 2: Set up the ratio of activation energies
We are given that the ratio of the activation energies is EfEb=2031. We can express Ef and Eb in terms of a variable x:
Ef=20xandEb=31x
Step 3: Substitute and solve for x
Substituting these expressions into the enthalpy equation:
−33.0=20x−31x
This simplifies to:
−33.0=−11x
Solving for x:
x=33.011=3.0
Step 4: Calculate Ef and Eb
Now we can find the values of Ef and Eb:
Ef=20x=20×3.0=60.0kJ mol−1
Eb=31x=31×3.0=93.0kJ mol−1
Step 5: Use the Arrhenius equation to find Ka
According to the Arrhenius equation, the rate constants for the forward and backward reactions are given by:
Kf=Ae−EfRTandKb=Ae−EbRT
The equilibrium constant Ka is given by:
Ka=KfKb=Ae−EfRTAe−EbRT=e−Ef−EbRT=e−60,000−93,000RT=e−−33,000RT
Step 6: Substitute values into the equation
Now substituting R=8.314J mol−1K−1=0.008314kJ mol−1K−1 and T=300K:
Ka=e−−33,0000.008314×300=e33,0002494.2
Calculating the exponent:
33,0002494.2≈13.24
Thus,
Ka=e13.24
Step 7: Calculate Ka
Using a calculator:
Ka≈5.572×105
Final Answer
The equilibrium constant Ka for the reaction at 300 K is approximately:
Ka≈5.572×105
The change in enthalpy (ΔH) for the reaction is related to the activation energies of the forward (Ef) and backward (Eb) reactions by the equation:
ΔH=Ef−Eb
Given that ΔH=−33.0kJ mol−1, we can express this as:
−33.0=Ef−Eb
We are given that the ratio of the activation energies is EfEb=2031. We can express Ef and Eb in terms of a variable x:
Ef=20xandEb=31x
Substituting these expressions into the enthalpy equation:
−33.0=20x−31x
This simplifies to:
−33.0=−11x
Solving for x:
x=33.011=3.0
Now we can find the values of Ef and Eb:
Ef=20x=20×3.0=60.0kJ mol−1
Eb=31x=31×3.0=93.0kJ mol−1
According to the Arrhenius equation, the rate constants for the forward and backward reactions are given by:
Kf=Ae−EfRTandKb=Ae−EbRT
The equilibrium constant Ka is given by:
Ka=KfKb=Ae−EfRTAe−EbRT=e−Ef−EbRT=e−60,000−93,000RT=e−−33,000RT
Now substituting R=8.314J mol−1K−1=0.008314kJ mol−1K−1 and T=300K:
Ka=e−−33,0000.008314×300=e33,0002494.2
Calculating the exponent:
33,0002494.2≈13.24
Thus,
Ka=e13.24
Using a calculator:
Ka≈5.572×105
The equilibrium constant Ka for the reaction at 300 K is approximately:
Ka≈5.572×105
Similar Questions
The energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1. Calculate Energy of activation for forward and backward reaction (EfandEa) at 300 K. Given that EfandEb are in the ratio 20 : 31. Assume that pre-exponential factor is same for forward and backward reaction.
View SolutionThe equilibrium constant (K) for the reaction. A+2B⇔2C+D is:
View SolutionThe energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1.
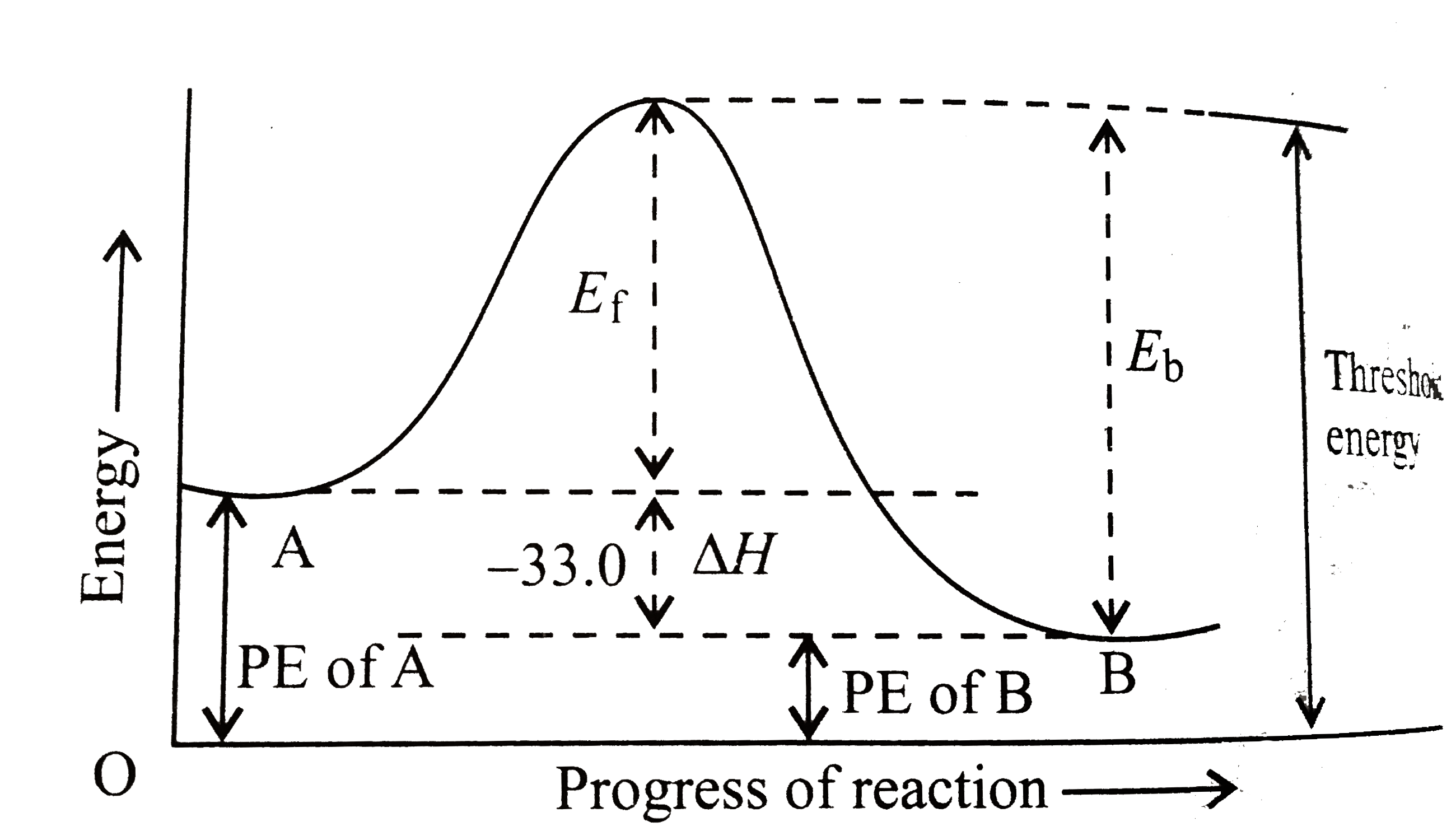
Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The equilibrium constant k for the reaction at 300K
View SolutionThe energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1.
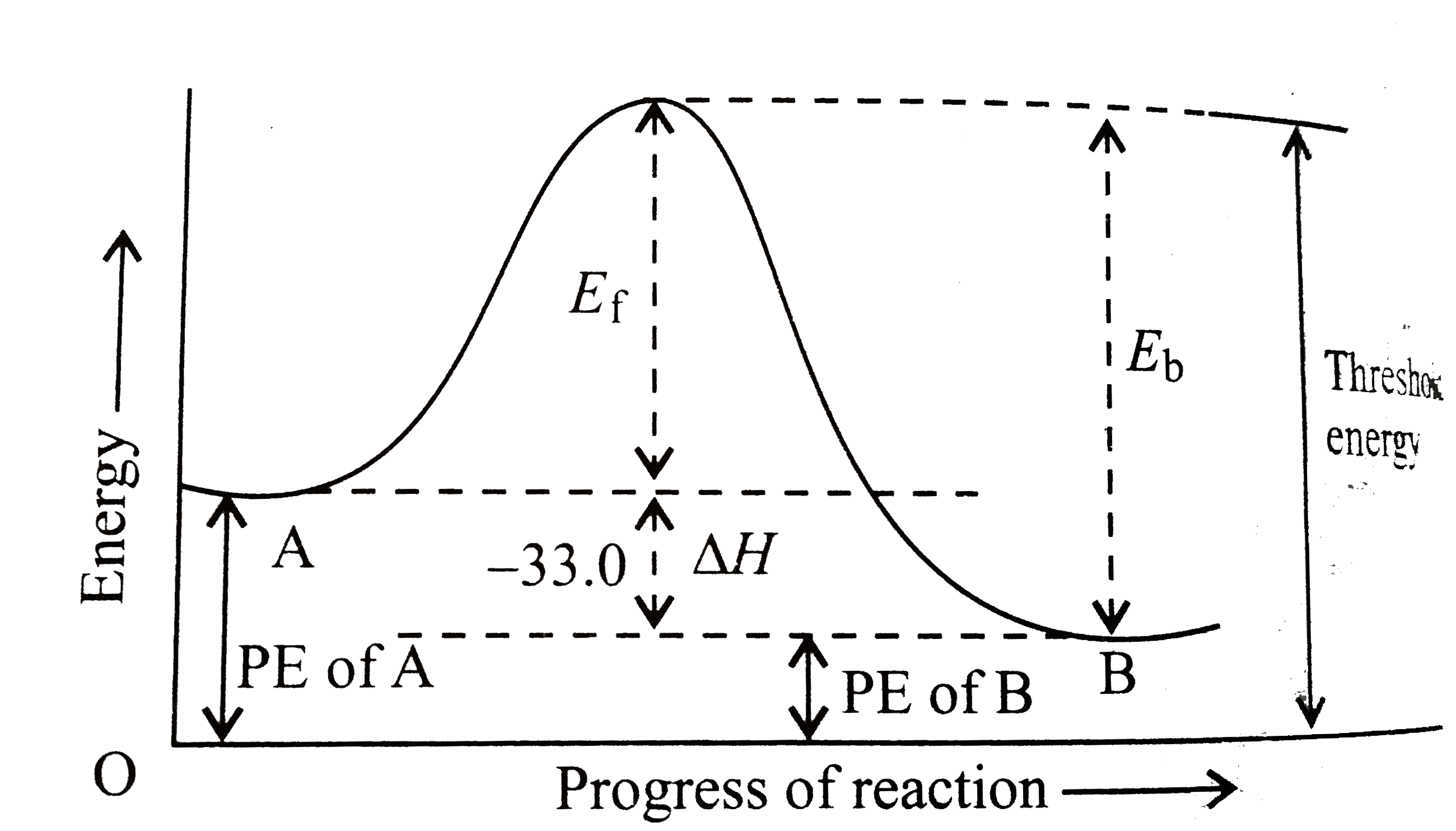
Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The threshold energy of the reaction is when PE of B is 30kJmol−1.
(a)30
(b)140
(c)123
(d) 125
View SolutionThe energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1.

Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The energy of activation for forward and backward reactions (Ef and Eb) at 300K. Given that Ef and Eb are in the ratio 20:31,
View SolutionThe unit of equilibrium constant Kc for the reaction A+B⇔C would be
View SolutionFor the reaction,
A⇔B,δH for the reaction is -33.0 kJ/mol.
Calculate
(i) Equilibrium constant Kc for the reaction at 300 K
(ii) If Ea(f)andEa(r) in the ratio 20:31 , calculate Ea(f) at 300 K .
Assuming pre-exponential factor same for forward and reverse reaction.
View SolutionThe equilibrium constant for the reactions
A+B⇔AB is 0.5 at 200K. The equilibrium constant for the reaction AB⇔A+B would be
View SolutionIf the equilibrium for a reaction is 4.0 what will be the equilibrium constant for the reverse reaction.
View SolutionA weak acid shows Ka = 0.0001. Calculate equilibrium constant for its reaction with strong base.
View Solution