The rate constant for a second order reaction is given by . The value of will be:
The correct Answer is:C
To find the activation energy Ea for the given second-order reaction, we can follow these steps:
Step 1: Write down the Arrhenius equation
The Arrhenius equation relates the rate constant k to the activation energy Ea:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant,
- T is the temperature in Kelvin.
Step 2: Compare the given equation with the Arrhenius equation
The given rate constant for the reaction is:
k=(5×1011)e−29000T
From this, we can identify:
- A=5×1011
- −EaR=−29000
Step 3: Rearrange to find Ea
From the comparison, we can express Ea as:
EaR=29000
Thus,
Ea=29000×R
Step 4: Substitute the value of R
The universal gas constant R is 8.314J/(mol K). Substituting this value in:
Ea=29000×8.314J/(mol K)
Step 5: Calculate Ea
Now we perform the multiplication:
Ea=29000×8.314=241106J/mol
Step 6: Convert Ea to kilojoules per mole
Since the options are given in kilojoules per mole, we convert joules to kilojoules:
Ea=241106J/mol×10−3kJ/J=241.106kJ/mol
Step 7: Round the answer
Rounding 241.106kJ/mol gives us:
Ea≈241kJ/mol
Final Answer
The value of Ea is approximately 241kJ/mol.
---
The Arrhenius equation relates the rate constant k to the activation energy Ea:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant,
- T is the temperature in Kelvin.
The given rate constant for the reaction is:
k=(5×1011)e−29000T
From this, we can identify:
- A=5×1011
- −EaR=−29000
From the comparison, we can express Ea as:
EaR=29000
Thus,
Ea=29000×R
The universal gas constant R is 8.314J/(mol K). Substituting this value in:
Ea=29000×8.314J/(mol K)
Now we perform the multiplication:
Ea=29000×8.314=241106J/mol
Since the options are given in kilojoules per mole, we convert joules to kilojoules:
Ea=241106J/mol×10−3kJ/J=241.106kJ/mol
Rounding 241.106kJ/mol gives us:
Ea≈241kJ/mol
The value of Ea is approximately 241kJ/mol.
Similar Questions
The rate constant of a reaction is given by k=2.1×1010exp(−2700/RT). It means that
View SolutionThe rate constant of a certain reaction is given by:
logk=5.4−212T+2.17logT
Calculate Eaat127∘C.
View SolutionThe value of rate constant for a second order reaction is 6.7×10−5mol−Ls− at 298 K and 1.64×10−4mol−Ls− at 313 K. Find the Arrhenius frequency factor A and activation energy of the reaction.
View SolutionThe value of rate constant for a second order reaction is 6.7×10−5mol−Ls− at 298 K and 1.64×10−4mol−Ls− at 313 K. Find the Arrhenius frequency factor A and activation energy of the reaction.
View SolutionThe value of rate constant for a second order reaction is 6.7×10−5mol−Ls− at 298 K and 1.64×10−4mol−Ls− at 313 K. Find the Arrhenius frequency factor A and activation energy of the reaction.
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
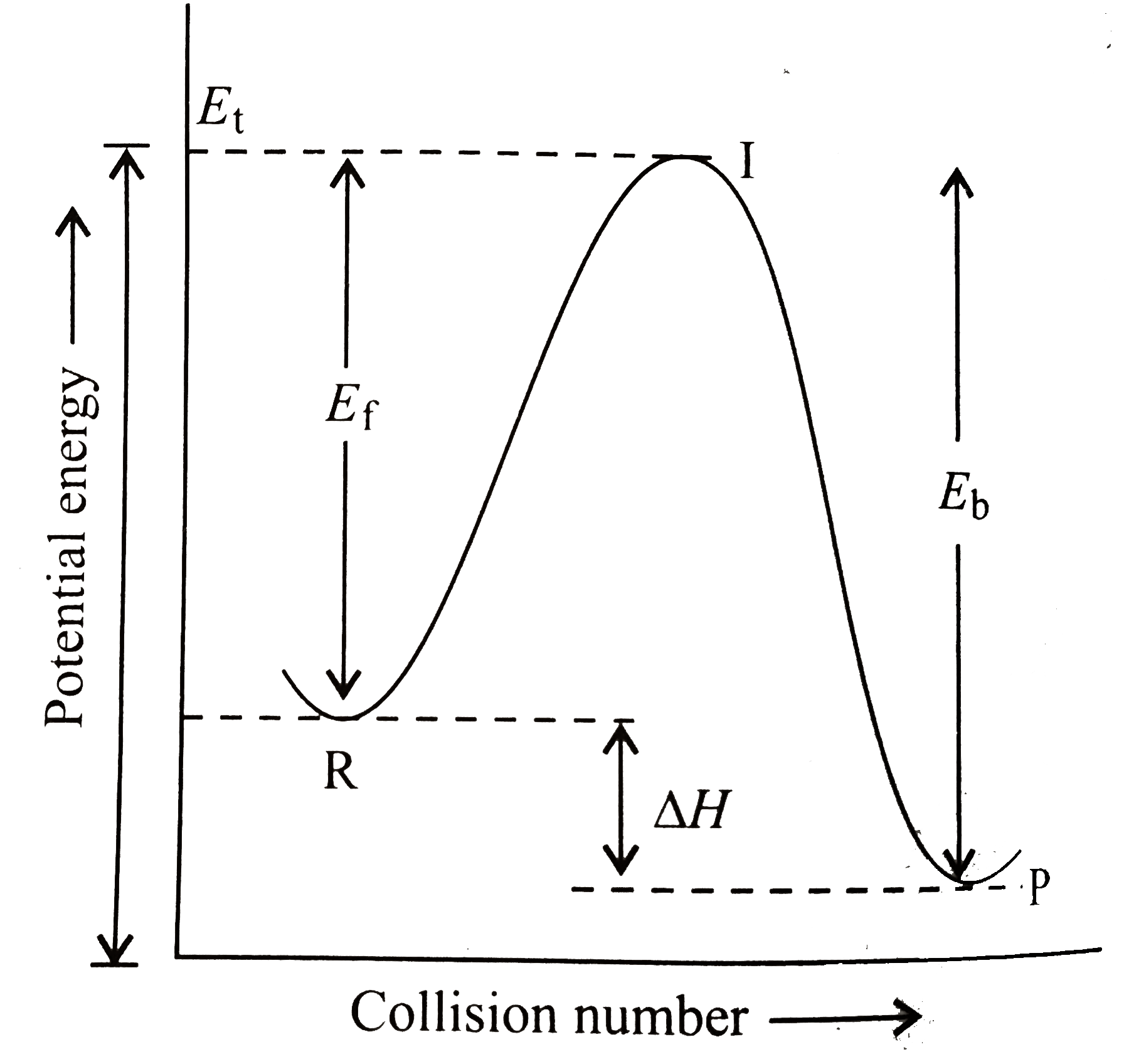
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The rate constant of a certain reaction is given by k=Ae−Ea/RT
(where A= Arrhenius constant). Which factor should be lowered so that the rate of reaction may increase?
View SolutionThe rate constant of a first order reaction is 10−3min−1 at 300K. The temperature coefficient of the reaction is 2. What is the rate constant of the reaction at 350K approximately ?
View SolutionA reaction rate constant is given by
k=1.2×1014e−2500RTs−1. It means
View SolutionIf the rate constant for a first order reaction is k, the time (t) required for the completion of 99% of the reaction is given by :
View SolutionThe rate constant k1 and k2 for two different reactions are 1016e−2000/T and 1015e−1000/T, respectively. The temperature at which k1=k2 is
View Solution
