F1andF2 are the two foci of the ellipse x29+y24=1. Let P be a point on the ellipse such that |PF1|=2|PF2|, where F1andF2 are the two foci of the ellipse . The area of △PF1F2 is :
3
4
√5
√132
The correct Answer is:B
Given |PF1|=2|PF2|
Also, |PF1|+|PF2|=6⇒|PF2|=2and|PF1|=4
Also b2=a2(1−e2)⇒4=a(1−a2)
⇒e=√53⇒F1F2=2√5
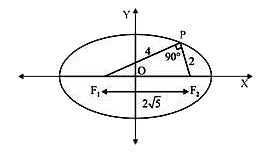
Now PF21+PF22=(F1F2)2⇒∠P=90∘
So , area (ΔPF1F2)=12(4×2)=4
Topper's Solved these Questions
- MOCK TEST 6BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 6EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- MOCK TEST 5BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 5EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- MOCK TEST 7BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 7EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
Similar Questions
The Foci of the ellipse x216+y225=1 are
View SolutionThe foci of the ellipse (x−3)236+(y+2)216=1, are
View SolutionFoci of ellipse (x−1)24+(y−2)29=1 is/are
View SolutionFind the foci of the ellipse 25(x+1)2+9(y+2)2=225.
View SolutionIf P is a point on the ellipse x236+y29=1, S and S ’ are the foci of the ellipse then find SP+S1P
View SolutionIf P is a point on the ellipse X29+y24=1
whose foci are S and S' then the value of PS + PS' is
View SolutionLet P be a variable on the ellipse x225+y216=1 with foci at F1andF2
View SolutionLet P be a point on the ellipse x2100+y225=1 and the length of perpendicular from centre of the ellipse to the tangent to ellipse at P be 5√2andF1andF2 be the foci of the ellipse, then PF1.PF2.
View Solutionif S and S are two foci of an ellipse x2a2+y2b2=1 (a<b) and P(x1,y1) a point on it then SP+ S'P is equal to
View SolutionP is any variable point on the ellipse 4x2+9y2=36 and F1,F2 are its foci. Maxium area of △PF1F2 ( e is eccentricity of ellipse )
View Solution