Let P={x:x∈R,|x|<2}
Q={x:x∈R,|x−1|≥2}
P∪Q=R−S then set S is : (where R is the set of real number)
[−2,2]
[2,3]
[2,3)
(−1,2]
The correct Answer is:C
To solve the problem, we need to analyze the sets P and Q and find the set S such that P∪Q=R−S.
Step 1: Define the set P
The set P is defined as:
P={x:x∈R,|x|<2}
This means that P includes all real numbers x such that the absolute value of x is less than 2.
To express this in interval notation, we can rewrite it as:
P=(−2,2)
P={x:x∈R,|x|<2}
This means that P includes all real numbers x such that the absolute value of x is less than 2.
P=(−2,2)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 2EXERCISE - PART III : MATHEMATICS (SECTION - 2)10videos
MOCK TEST 2
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 13EXERCISE - MATHEMATICS( SECTION-2)5videos
MOCK TEST 13
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 3EXERCISE - PART III : MATHEMATICS (SECTION-2)10videos
MOCK TEST 3
Similar Questions
Let A={x:x∈R,−1<x<1}, B={x:x∈R,x≤0orx≥2} and A∪B=R−D, then find set D
View SolutionIf P={x:7x−4>5x+2,x∈R}andQ={x:x−19≥1−3x,x∈R}, find the range of set P∩Q and represent it on a number line.
View SolutionLet R1={(x,y)∈R×R:x=λy⇒λ∈Q} is a relation, R is set of real numbers then R1 is
View SolutionIf f:R→R,f(x)=x3andg:R→R,g(x)=2x2+1, and R is the set of real numbers then find fog(x) and gof (x).
View SolutionLet f:R→R be given by f(x)={5x ,if x in Q ,x^ 2 + 6,ifx∈R−Q then
View SolutionP is solution set of :7x−2>4x+1andQ is the solution set of : 9x−45≥5(x−5): where x∈R.
Represent (i) P - Q and P∩Q on different number lines.View SolutionP is the solution set of 7x−2>4x+1andQ is the solution set of 9x−45≥5(x−5), where x∈R. Represent :
P∩Q' on different number lines.View SolutionGiven P={x:9<2x−1≤13,x∈R}andQ={x:−5≤3+4x<15,x∈I}Where R={Real Numbers} and I={Integers}.Represent P and Q on number lines. Write down the elements of P∩Q
View SolutionIn Figure , find out ∠PXR, if PQ ∣∣ RS.
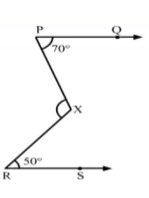 View Solution
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.
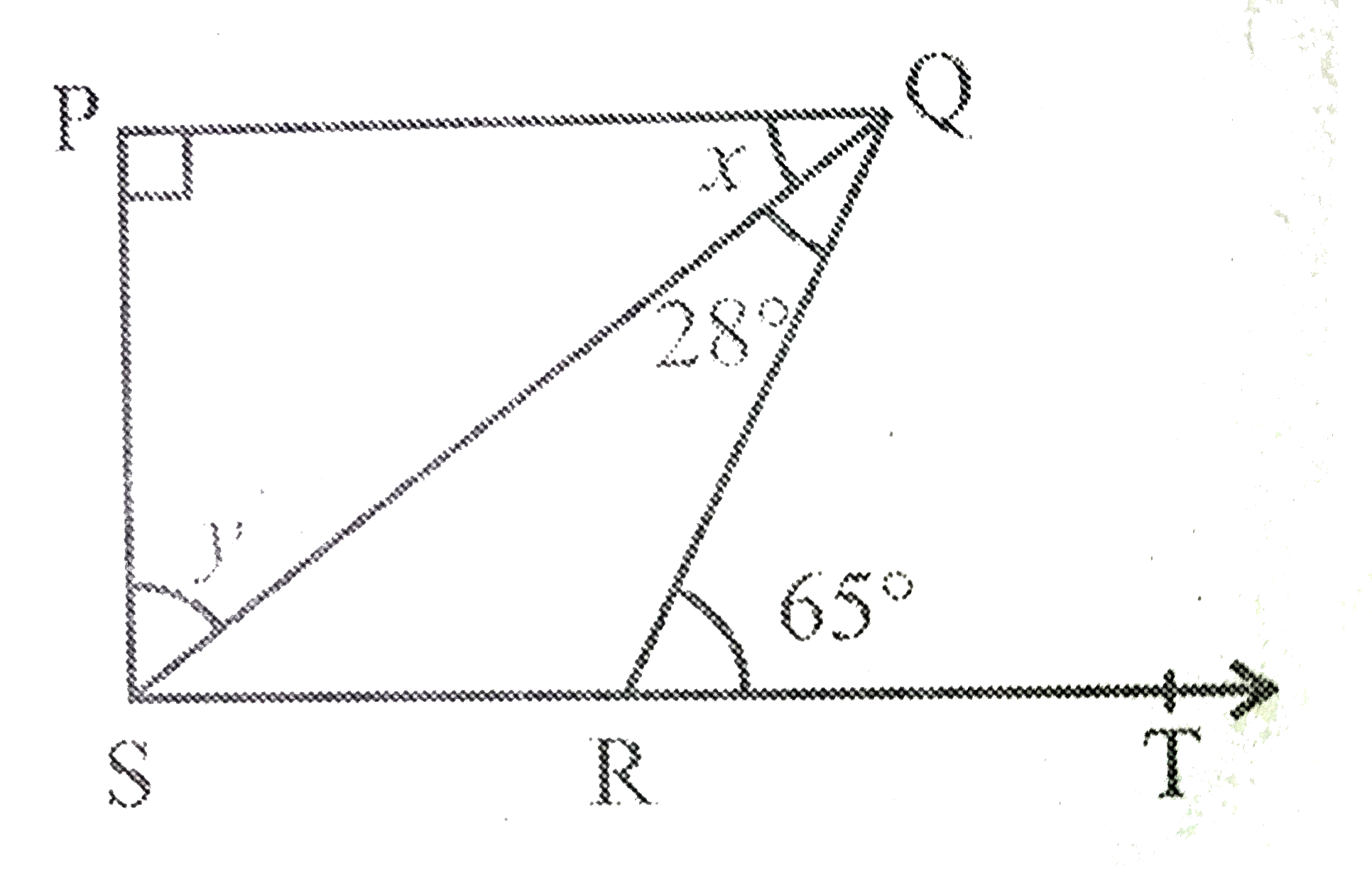 View Solution
View Solution

