Two particles of mass m & 2m have velocities uˆj & uˆi respectively . They collide completely inelastically. Find the loss in kinetic energy of the system.
mu2
23mu2
mu24
mu24
The correct Answer is:B
To solve the problem of finding the loss in kinetic energy during a completely inelastic collision between two particles of masses m and 2m with initial velocities u^j and u^i respectively, we can follow these steps:
Step 1: Calculate the Initial Kinetic Energy
The initial kinetic energy (KEinitial) of the system can be calculated using the formula:
KE=12mv2
For the first particle (mass m with velocity u^j):
KE1=12m(u2)=12mu2
For the second particle (mass 2m with velocity u^i):
KE2=12(2m)(u2)=mu2
Thus, the total initial kinetic energy is:
KEinitial=KE1+KE2=12mu2+mu2=12mu2+22mu2=32mu2
Step 2: Calculate the Final Velocity After Collision
In a completely inelastic collision, the two particles stick together. We can use conservation of momentum to find the final velocity (v) of the combined mass.
The initial momentum (pinitial) is:
pinitial=mu^j+2mu^i=2mu^i+mu^j
The total mass after collision is:
M=m+2m=3m
Using conservation of momentum:
pinitial=pfinal⇒2mu^i+mu^j=3mv
Thus, we can solve for v:
v=2mu^i+mu^j3m=2u^i+u^j3
Step 3: Calculate the Final Kinetic Energy
The final kinetic energy (KEfinal) can be calculated using the final velocity:
KEfinal=12Mv2=12(3m)v2
First, we need to find v2:
v2=(2u^i+u^j3)⋅(2u^i+u^j3)=19((2u)2+(u)2)=19(4u2+u2)=5u29
Now substituting back:
KEfinal=12(3m)(5u29)=15mu218=5mu26
Step 4: Calculate the Loss in Kinetic Energy
The loss in kinetic energy (ΔKE) is given by:
ΔKE=KEinitial−KEfinal=32mu2−56mu2
Converting 32mu2 to a common denominator:
32mu2=96mu2
Thus:
ΔKE=96mu2−56mu2=46mu2=23mu2
Final Answer
The loss in kinetic energy of the system is:
ΔKE=23mu2
The initial kinetic energy (KEinitial) of the system can be calculated using the formula:
KE=12mv2
For the first particle (mass m with velocity u^j):
KE1=12m(u2)=12mu2
For the second particle (mass 2m with velocity u^i):
KE2=12(2m)(u2)=mu2
Thus, the total initial kinetic energy is:
KEinitial=KE1+KE2=12mu2+mu2=12mu2+22mu2=32mu2
In a completely inelastic collision, the two particles stick together. We can use conservation of momentum to find the final velocity (v) of the combined mass.
pinitial=mu^j+2mu^i=2mu^i+mu^j
The total mass after collision is:
M=m+2m=3m
Using conservation of momentum:
pinitial=pfinal⇒2mu^i+mu^j=3mv
Thus, we can solve for v:
v=2mu^i+mu^j3m=2u^i+u^j3
The final kinetic energy (KEfinal) can be calculated using the final velocity:
KEfinal=12Mv2=12(3m)v2
First, we need to find v2:
v2=(2u^i+u^j3)⋅(2u^i+u^j3)=19((2u)2+(u)2)=19(4u2+u2)=5u29
Now substituting back:
KEfinal=12(3m)(5u29)=15mu218=5mu26
The loss in kinetic energy (ΔKE) is given by:
ΔKE=KEinitial−KEfinal=32mu2−56mu2
Converting 32mu2 to a common denominator:
32mu2=96mu2
Thus:
ΔKE=96mu2−56mu2=46mu2=23mu2
The loss in kinetic energy of the system is:
ΔKE=23mu2
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 13EXERCISE - PHYSICS ( SECTION -2)5videos
MOCK TEST 13
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 12EXERCISE - PHYSICS (SECTION 2)5videos
MOCK TEST 12
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 2EXERCISE - PART I : PHYSICS (SECTION - 2)10videos
MOCK TEST 2
Similar Questions
Two particles of equal mass m are moving with velocities vˆi and v(ˆi+ˆj2) respectively. If the particles collide completely inelastically, then the energy lost in the process is
View SolutionTwo particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionTwo particles of mass 1 kg and 2 kg are moving with speed 2 m/s and 5 m/s as shown in the figure, they collides perfectly inelastically. And second particle come to rest after collision. Find
(a) Their final velocity
(b) Loss in kinetic energy
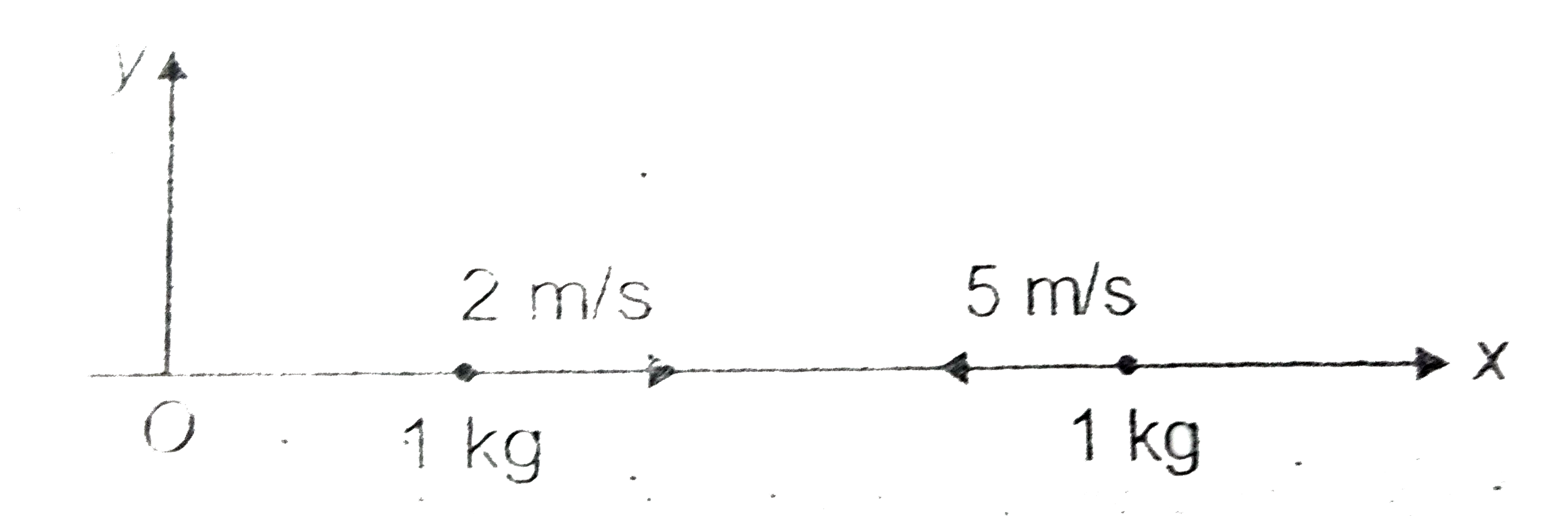 View Solution
View SolutionA ball of mass '2m' moving with velocity uˆi collides with another ball of mass 'm' moving with velocity −2uˆi. After the collision, mass 2m moves with velocity u2(ˆi−ˆj). Then the change in kinetic energy of the system ( both balls ) is
View SolutionTwo bodies of 6kg and 4kg masses have their velocity 5ˆi−2ˆj+10ˆk and 10ˆi−2ˆj+5ˆk respectively. Then, the velocity of their centre of mass is
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
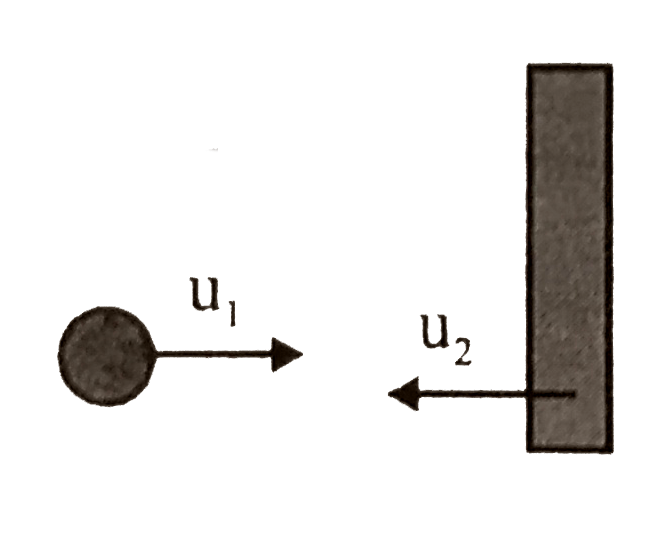 View Solution
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionFind the equation of the sphere described on the joint of points AandB having position vectors 2ˆi+6ˆj−7ˆkand−2ˆi+4ˆj−3ˆk, respectively, as the diameter. Find the center and the radius of the sphere.
View Solution

