If b and c are lengths of the segments of any focal chord of the parabola y2=4ax, then write the length of its latus rectum.
b+c2
bcb+c
2bcb+c
√bc
The correct Answer is:C
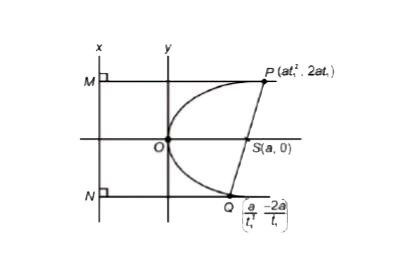
Let P(at21,2at1)andQ(at22,2at2) are end points of a chord
PQ is a focal chord
t1t2=−1
t2=−1t1
Q(at21,−2at1)
b=SP=PM=a+at21
b−a=at21...........(i)
c=SQ=QN=a+at21
c−a=at21...........(ii)
Similar Questions
Of the parabola, 4(y−1)2=−7(x−3) find
The length of the latus rectum.
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf aandc are the lengths of segments of any focal chord of the parabola y2=2bx,(b>0), then the roots of the equation ax2+bx+c=0 are (a) real and distinct (b) real and equal (c) imaginary (d) none of these
View SolutionPQ is any focal chord of the parabola y2=8x. Then the length of PQ can never be less than _________ .
View SolutionIf the length of a focal chord of the parabola y2=4ax at a distance b from the vertex is c, then prove that b2c=4a3.
View SolutionIf the parabola y2=4ax passes through the point (3,2) then find the length of its latus rectum.
View SolutionIf the parabola y2=4ax passes through the point (3,2) then find the length of its latus rectum.
View SolutionIf the parabola y2=4ax passes through the point (4,5), find the length of its latus rectum.
View Solution
