The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
A
√22
B
√32
C
12
D
34
Video Solution
Text Solution
The correct Answer is:C
Let the equation of E2 be
x2a2+y2b2=1
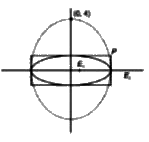
Clearly the point P has coordinates (3,2)
So, (3,2) and (0,4) satisfy E2
16b2=1⇒b2=16
And 9a2+4b2=1
9a2=34⇒a2=12
e=√1−1216=12
|
Similar Questions
The eccentricity of te ellipse x216+y24=1 is _______
View Solutionthe equation of the ellipse passing through (2,1) having e=1/2 , is
View SolutionThe eccentricity of ellipse 4(x−2y+1)2+9(2x+y+2)2=180 is
View SolutionThe eccentricity of the ellipse 4x2+9y2=36 is a.12√3 b. 1√3 c. √53 d. √56
View SolutionThe eccentricity of the ellipse 4x2+9y2=36 is
a.12√3
b. 1√3
c. √53
d. √56
View SolutionThe eccentricity of the ellipse, which passes through the points (2, −2) and (−3,1) is :
View SolutionThe eccentricity of the ellipse 4x2+9y2+8x+36y+4=0 is a.56 b. 35 c. √23 d. √53
View SolutionIf e' is the eccentricity of the ellipse x2a2+y2b2=1 (a>b), then
View SolutionThe eccentricity of the ellipse 5x2+9y2=1 is a.2/3 b. 3/4 c. 4/5 d. 1/2
View SolutionThe eccentricity of the ellipse 5x2+9y2=1 is a.2/3 b. 3/4 c. 4/5 d. 1/2
View Solution
