A cubical block is floating inside a bath. The temperature of system is increased by small temperature δ(T). It was found that the depth of submerged portion of cube does not change. Find the relation between coefficient of linear expansion (α) of the cube and volume expansion of liquid (γ). 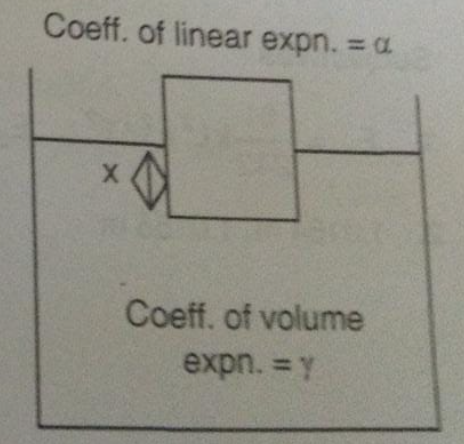
Step by step video & image solution for A cubical block is floating inside a bath. The temperature of system is increased by small temperature delta(T). It was found that the depth of submerged portion of cube does not change. Find the relation between coefficient of linear expansion (alpha) of the cube and volume expansion of liquid (gamma). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A glass vessel of volume v0 is completely filled with a liquid and its temperature is raised by ΔT. What volume of the liquid will overflow? Coefficient of linear expansion of glass =α−(g) and coefficient of volume expansion of the liquid =γc
View SolutionThe moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View Solution
Knowledge Check
Find the temperature at which the fundamental frequency of an organ pipe is independent of small variation in temperature in terms of the coefficient of linear expansion ( α) of the material of the tube.
A1/3αB1/2αC1/4αD1/5α
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beAαA=3×10−6/∘C,500∘CBαA=3×10−6/∘C,222.22∘CCαA=27×10−6/∘C,500∘CDαA=27×10−6/∘C,222.22∘CThe moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
A beaker contains a liquid of volume V0. A solid block of volume V floats in the liquid with 90% of its volume submerged in the liquid. The whole system is heated to raise its temperature by Δθ. It is observed that the height of liquid in the beaker does not change and the solid in now floating with its entire volume submerged. Calculate Δθ. It is given that coefficient of volume expansion of the solid and the glass (beaker) are γs and γg respectively.

View SolutionIt was found that resistance of a cylindrical specimen of a wire does not change with small change in temperature. If its temperature coefficient of resistivity is αR then find its thermal expansion coefficient (α).
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA thread of liquid is in a uniform capillary tube of length L. As measured by a ruler. The temperature of the tube and thread of liquid is raised by ΔT. If γ be the coefficient of volume expansion of the liquid and α be the coefficient of linear expansion of the material of the tube, then the increase ΔL in the length of the thread, again measured by the ruler will be
View Solution
