Solution set of (5x−1)<(x+1)2<(7x−3) is
(1, 4)
[2, 4]
(2, 4)
(−∞,1)∪(2,∞)
The correct Answer is:C
To solve the inequality (5x−1)<(x+1)2<(7x−3), we will break it down into two parts:
1. Solve 5x−1<(x+1)2
2. Solve (x+1)2<7x−3
Step 1: Solve 5x−1<(x+1)2
1. Expand the right side:
5x−1<x2+2x+1
2. Rearrange the inequality:
5x−1−x2−2x−1<0
−x2+3x−2<0
Multiplying through by -1 (reversing the inequality):
x2−3x+2>0
3. Factor the quadratic:
(x−1)(x−2)>0
4. Determine the intervals:
- The roots are x=1 and x=2.
- Test intervals: (−∞,1), (1,2), (2,∞).
- For x<1: Choose x=0 → (0−1)(0−2)>0 → True.
- For 1<x<2: Choose x=1.5 → (1.5−1)(1.5−2)<0 → False.
- For x>2: Choose x=3 → (3−1)(3−2)>0 → True.
5. Solution for this part:
x∈(−∞,1)∪(2,∞)
Step 2: Solve (x+1)2<7x−3
1. Expand the left side:
x2+2x+1<7x−3
2. Rearrange the inequality:
x2+2x+1−7x+3<0
x2−5x+4<0
3. Factor the quadratic:
(x−4)(x−1)<0
4. Determine the intervals:
- The roots are x=1 and x=4.
- Test intervals: (−∞,1), (1,4), (4,∞).
- For x<1: Choose x=0 → (0−4)(0−1)>0 → False.
- For 1<x<4: Choose x=2 → (2−4)(2−1)<0 → True.
- For x>4: Choose x=5 → (5−4)(5−1)>0 → False.
5. Solution for this part:
x∈(1,4)
Step 3: Combine the solutions
Now we have two conditions:
1. x∈(−∞,1)∪(2,∞)
2. x∈(1,4)
To find the intersection of these two sets:
- The overlapping region is (2,4).
Final Solution
Thus, the solution set for the inequality (5x−1)<(x+1)2<(7x−3) is:
x∈(2,4)
2. Solve (x+1)2<7x−3
5x−1<x2+2x+1
5x−1−x2−2x−1<0
−x2+3x−2<0
Multiplying through by -1 (reversing the inequality):
x2−3x+2>0
(x−1)(x−2)>0
- The roots are x=1 and x=2.
- Test intervals: (−∞,1), (1,2), (2,∞).
- For x<1: Choose x=0 → (0−1)(0−2)>0 → True.
- For 1<x<2: Choose x=1.5 → (1.5−1)(1.5−2)<0 → False.
- For x>2: Choose x=3 → (3−1)(3−2)>0 → True.
x∈(−∞,1)∪(2,∞)
x2+2x+1<7x−3
x2+2x+1−7x+3<0
x2−5x+4<0
(x−4)(x−1)<0
- The roots are x=1 and x=4.
- Test intervals: (−∞,1), (1,4), (4,∞).
- For x<1: Choose x=0 → (0−4)(0−1)>0 → False.
- For 1<x<4: Choose x=2 → (2−4)(2−1)<0 → True.
- For x>4: Choose x=5 → (5−4)(5−1)>0 → False.
x∈(1,4)
1. x∈(−∞,1)∪(2,∞)
2. x∈(1,4)
- The overlapping region is (2,4).
x∈(2,4)
Topper's Solved these Questions
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Section I - Solved Mcqs
20 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- ALGEBRA OF VECTORSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Chapter Test
30 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
Similar Questions
Knowledge Check
The solution set of x−13+4<(x−55)−2 is
A(−∞,−50)B(−∞,−5)C(−∞,−10)D(−∞,−15)The solution set of 2x+13<3x−25x∈R on the number line is
A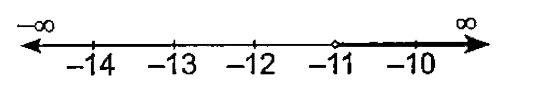 B
B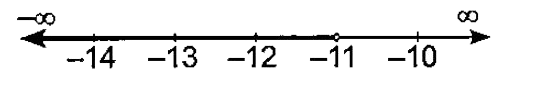 C
C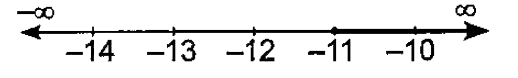 D
D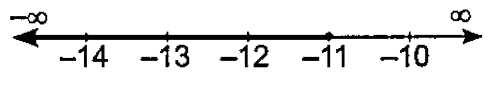
The solution set of −812<−12−4x<712,x∈W on the number line is:
A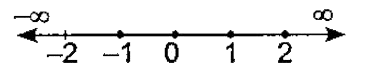 B
B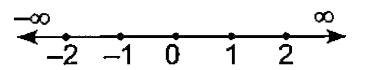 C
C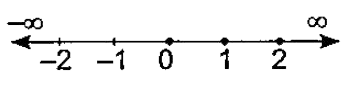 D
D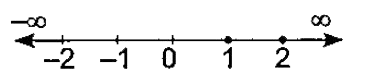
The number of intergal values of x if 5x−1<(x+1)2<7x−3 is
View SolutionFind the solution set of (x−1)(x−2)(x−3)2(x−4)2(x−5)3<0
View SolutionThe solution set of −1<3−2x<9,x∈I is .....
View SolutionThe solution set of −12<4−3x−5≤2,x∈R is
View SolutionThe solution set of −223<x+13≤313,x∈R is
View Solution
