Question

OPQR is a square and M,N are the middle points of the sides of PQ nad QR, respectively,then the ratio of the area of the square to that of triangle OMN is

Options

A. `4:1`
B. `2:1`
C. `8:3`
D. `4:3`

Answer

C

Explanation

Taking the coordinates of the vertics of O,P,Q and R as O(0,0)P (a,0), Q(a,a) and R (0,a) respectively, we get the coordinates of M and N as (a,a/2) and (a/2/a) respectively.

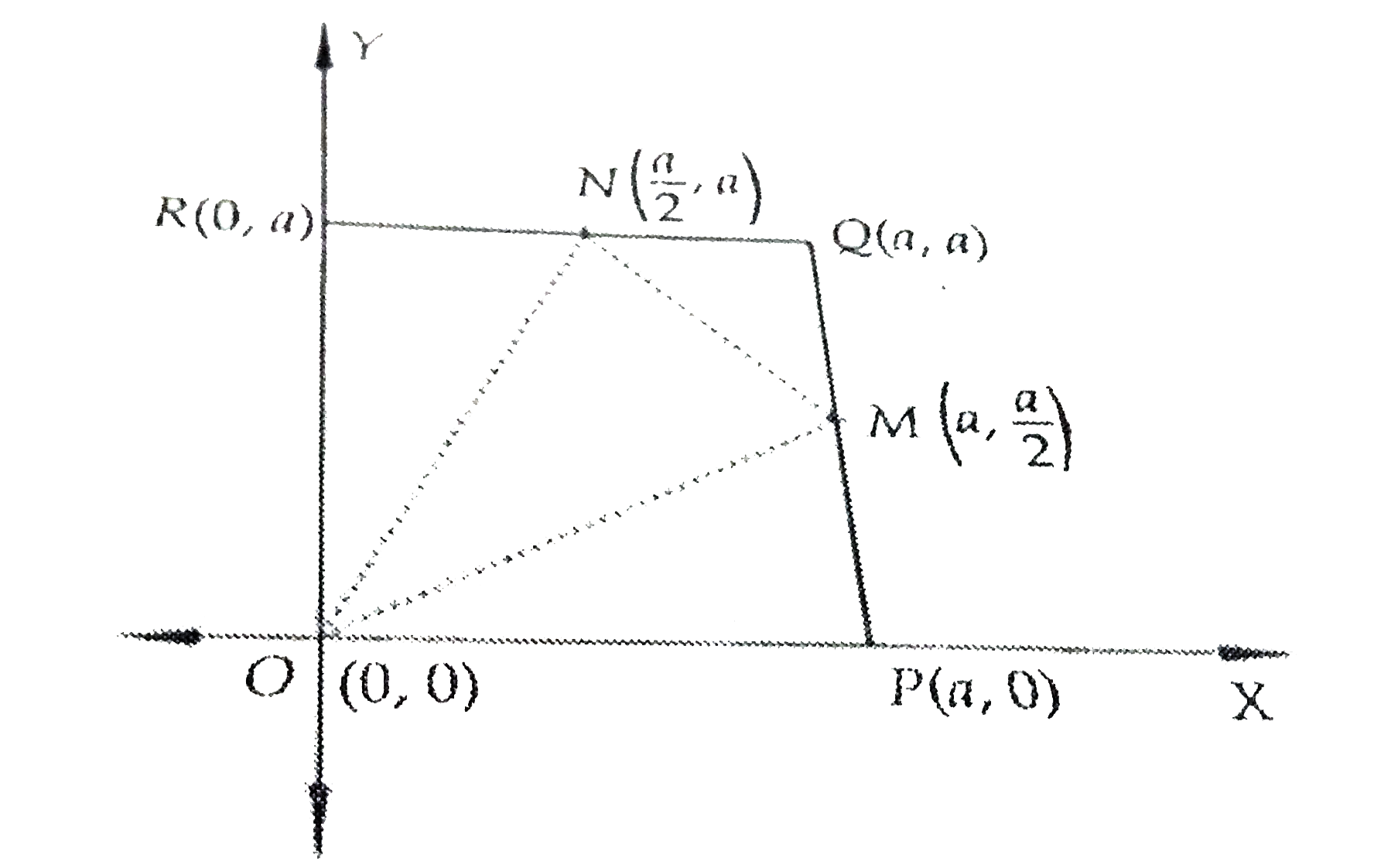
`:. "Area of" DeltaOMN=(1)/(2)|{:(a,0,1),(a,a//2,1),(a//2,a,1):}|=(3)/(8)a^(2)`
`:.` Required ratio `=8:3`