A man invites a party to (m+n) friends to dinner and places m at one round table and n at another. The number of ways of arranging the guests is
(m+n)!m!n!
(m+n)!(m−1)!(n−1)!
(m−1)!(n−1)!
none of these
The correct Answer is:D
To solve the problem of arranging (m+n) friends at two round tables, one with m friends and the other with n friends, we can follow these steps:
1. Select m Friends for the First Table:
We need to choose m friends from a total of (m+n) friends. The number of ways to do this is given by the combination formula:
(m+nm)
2. Select n Friends for the Second Table:
After selecting m friends, the remaining friends will automatically be n (since m + n - m = n). The number of ways to select these n friends from the remaining n friends is:
(nn)=1
(There is only one way to select all n friends.)
3. Arrange m Friends at the First Round Table:
For arranging m friends at a round table, we fix one friend and arrange the remaining (m-1) friends. The number of arrangements is:
(m−1)!
4. Arrange n Friends at the Second Round Table:
Similarly, for arranging n friends at the second round table, we fix one friend and arrange the remaining (n-1) friends. The number of arrangements is:
(n−1)!
5. Combine All the Steps:
Now, we combine all the ways to select and arrange the friends:
Total Ways=(m+nm)×(m−1)!×1×(n−1)!
6. Simplifying the Expression:
We can simplify this expression. The combination can be expressed as:
(m+nm)=(m+n)!m!n!
Thus, the total number of arrangements becomes:
Total Ways=(m+n)!m!n!×(m−1)!×(n−1)!
7. Final Simplification:
Now, we can cancel out the factorials:
=(m+n)!m⋅n
Final Answer:
The total number of ways to arrange the guests is:
(m+n)!m⋅n
We need to choose m friends from a total of (m+n) friends. The number of ways to do this is given by the combination formula:
(m+nm)
After selecting m friends, the remaining friends will automatically be n (since m + n - m = n). The number of ways to select these n friends from the remaining n friends is:
(nn)=1
(There is only one way to select all n friends.)
For arranging m friends at a round table, we fix one friend and arrange the remaining (m-1) friends. The number of arrangements is:
(m−1)!
Similarly, for arranging n friends at the second round table, we fix one friend and arrange the remaining (n-1) friends. The number of arrangements is:
(n−1)!
Now, we combine all the ways to select and arrange the friends:
Total Ways=(m+nm)×(m−1)!×1×(n−1)!
We can simplify this expression. The combination can be expressed as:
(m+nm)=(m+n)!m!n!
Thus, the total number of arrangements becomes:
Total Ways=(m+n)!m!n!×(m−1)!×(n−1)!
Now, we can cancel out the factorials:
=(m+n)!m⋅n
The total number of ways to arrange the guests is:
(m+n)!m⋅n
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
A gentlemen hosts a party of (m+n) guests and places 'm' at one round table and the remaining 'n' at the other round table. Number of ways the guests can be arranged is
View SolutionHarsha invites 13 guests to a dinner and places 8 of them at one table and remaining 5 at the other, the table being round. The number of ways he can arrange the guests is
View Solution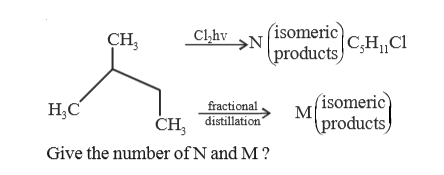
Give the number of N and M ?
View Solution
Give the number of N and M ?
View SolutionA person invites a group of 10 friends at dinner and sits 5 on a round table and 5 more on another round table, 4 on one round table and 6 on the other round table. Find the number of ways in each case in which he can arrange the guest.
View SolutionA person invites a group of 10 friends at dinner and sits (i) 5 on a round table and 5 on other round table (ii) 4 on one round table 6 on other round table . Find no. of ways in each case in which he can arrange the guest?
View SolutionThere are n seats round a table numbered 1,2,3,...,n. The number of ways in which m(≤n) persons can take seats is
View Solution2m white counters and 2n red counters are arranged in a straight line with (m+n) counters on each side of central mark. The number of ways of arranging the counters, so that the arrangements are symmetrical with respect to the central mark is (A) .m+nCm (B) .2m+2nC2m (C) 12(m+n)!m!n! (D) None of these
View SolutionIn how many ways can 5 friends of a man be seated on a round table and 4 friends on other round table out of 9 friends?
View SolutionA lady gives a dinner party to 5 guests to be selected from nine friends. The number of ways of forming the party of 5, given that two of the friends will not attend the party together, is
View Solution
