Suppose If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y = x, then g(x) equals
The correct Answer is:D
For all we have
Therefore, is a bijection and hence invertible.
It is given that g(x) is the function whose graph is the reflection of the graph, of f(x) with respect to the line y=x. This means that g(x) is the inverse of f(x).

Topper's Solved these Questions
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Section II - Assertion Reason Type
10 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise
48 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test
29 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
- HYPERBOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - HYPERBOLAEXERCISE - Chapter Test
29 Videos
Similar Questions
Suppose f(x)=(x+1)2 forx≥−1. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y=x, then g(x) equal. (a)1−√x−1,x≥0 (b) 1(x+1)2,x>−1 (c)√x+1,x≥−1 (d) √x−1,x≥0
View SolutionSuppose f(x)=(x+1)2forx≥−1. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y=x, then g(x) equal. a−√x−1,x≥0 (b) 1(x+1)2,x≻1 √x+1,x≥−1 (d) √x−1,x≥0
View SolutionIf g(x) is a curve which is obtained by the reflection of f(x)=ex−e−x2 then by the line y=x then
View SolutionIf g(x) is a curve which is obtained by the reflection of f(x)=ex−e−x2 then by the line y=x then
View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
View SolutionConsider the following function f whose graph is given below.
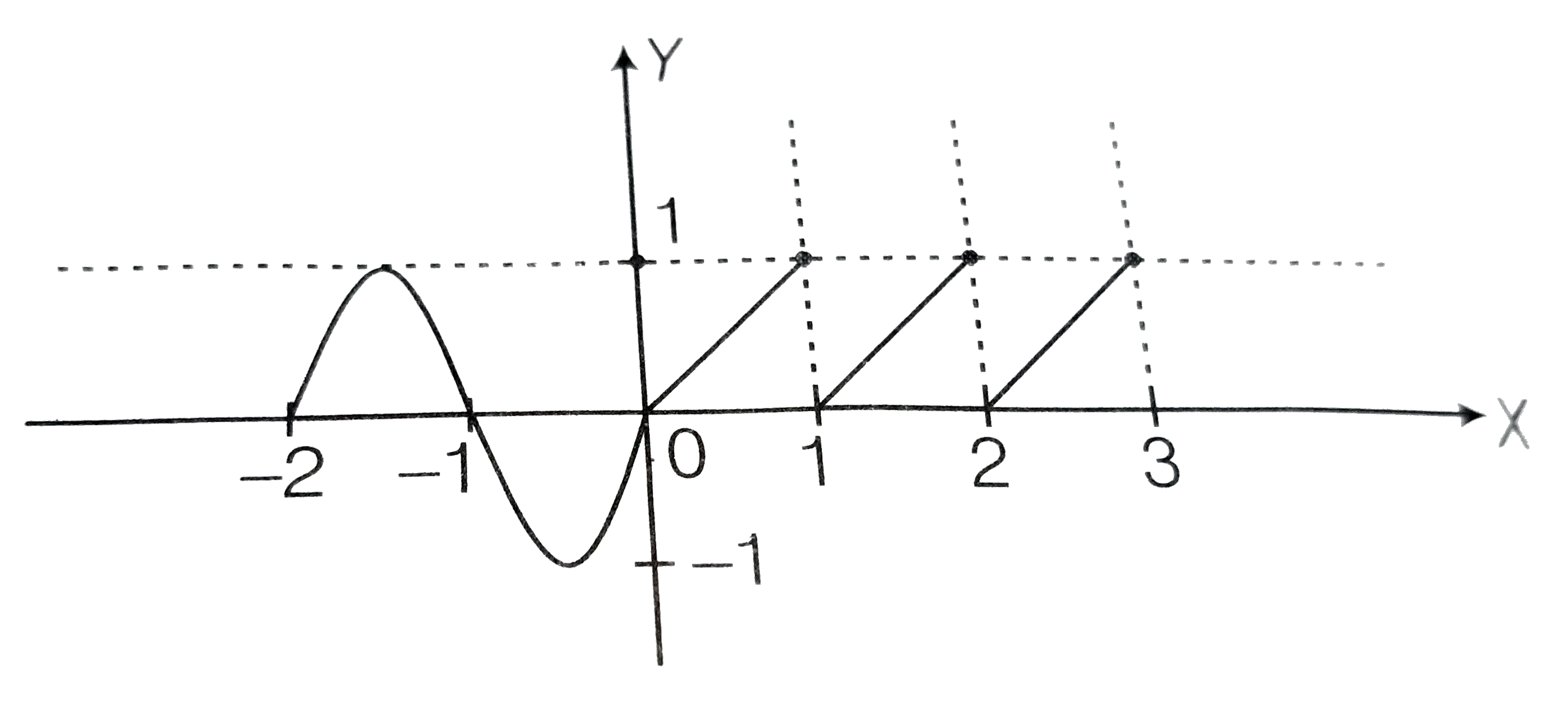
Draw the graph of following functions.
(g) 2f(x)
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionConsider the following function f whose graph is given below.
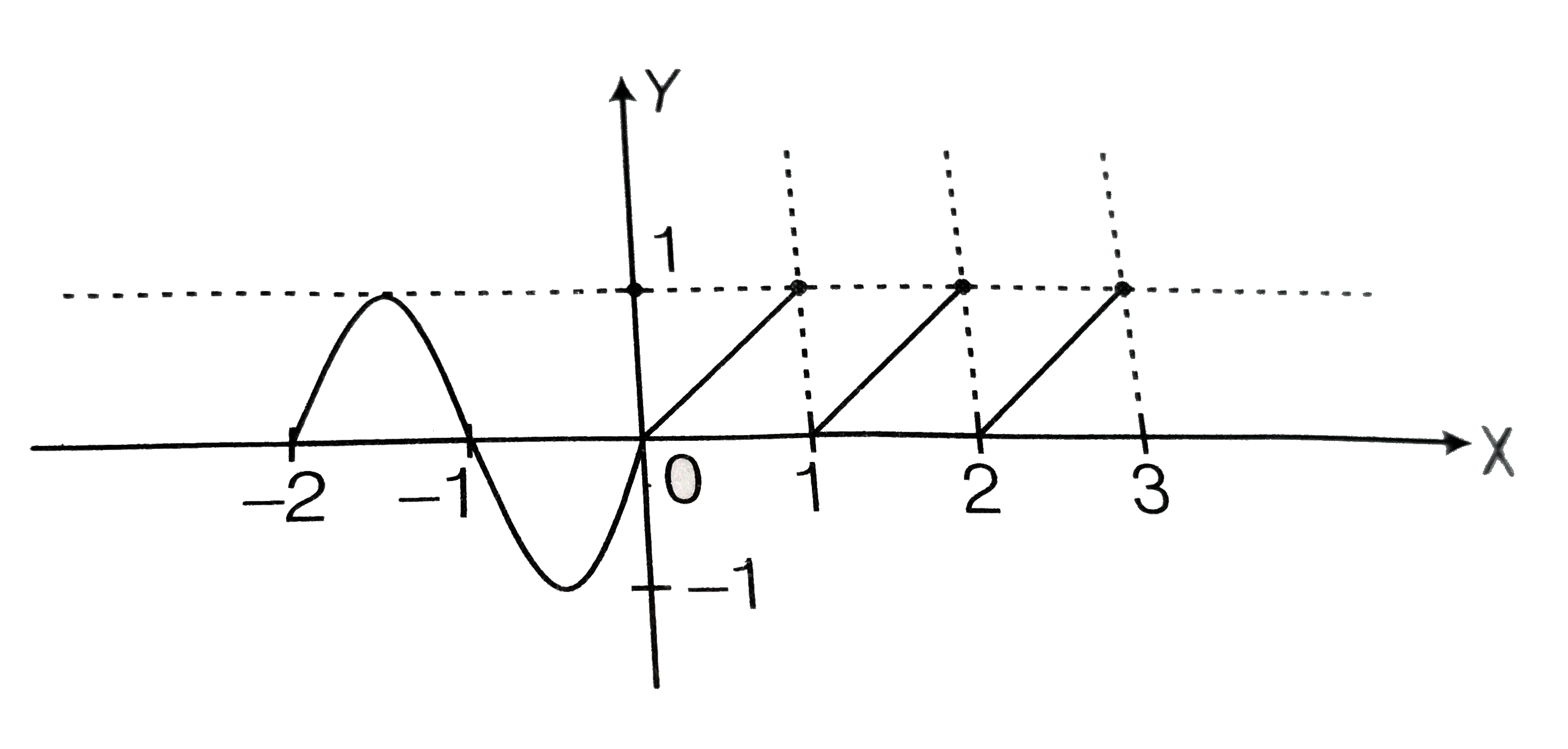
Draw the graph of following functions.
(g) f(x−[x])
View SolutionConsider a function f(x)=xx,∀x∈[1,∞). If g(x) is the inverse function of f(x), then the value of g'(4) is equal to
View Solution
