Let f:(−1,1)→B be a function defined by f(x)=tan−1(2x)1−x2 . Then f is both one-one and onto when B is the interval. [0,π2) (b) (0,π2) (−π2,π2) (d) [−π2,π2]
(−π/2,π/2)
[−π/2,π/2]
[0,π/2]
(0,π/2)
The correct Answer is:A
We have
f(x)=tan−1(2x1−x2)=2tan−1x,ifx∈(−1,1)
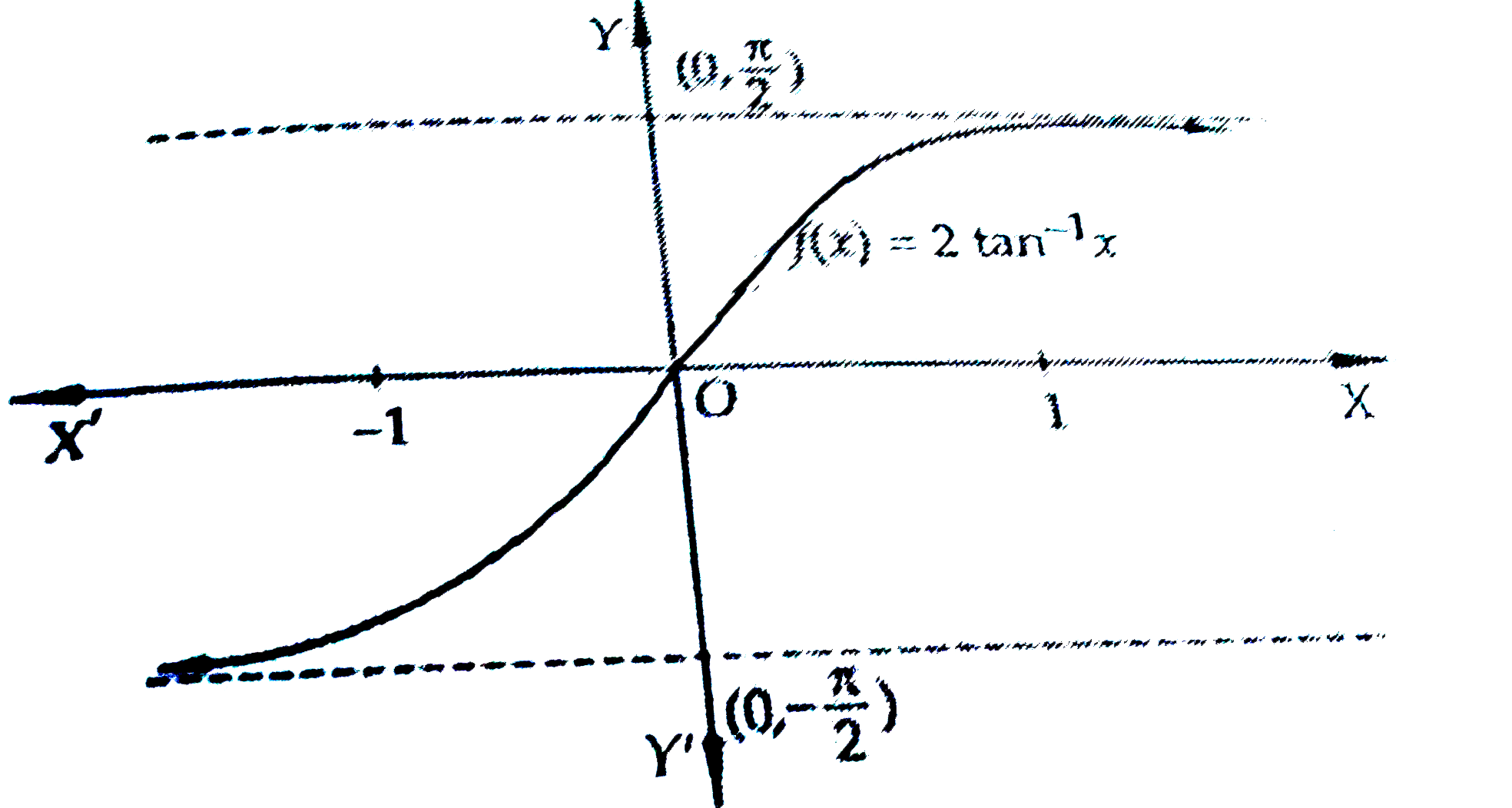
Since, f(x) is both one-one both and onto. Therefore,
B=Range (f)=(f(−1)),f(1))=(−π/2,π/2)
Topper's Solved these Questions
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Section II - Assertion Reason Type
10 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise
48 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test
29 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
- HYPERBOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - HYPERBOLAEXERCISE - Chapter Test
29 Videos
Similar Questions
Let f:(−1,1)→B be a function defined by f(x)=tan−1[2x1−x2] . Then f is both one-one and onto when B is the interval. (a)[0,π2) (b) (0,π2) (c)(−π2,π2) (d) [−π2,π2]
View SolutionLet f:R→B, be a function defined f(x)=tan−1.2x√3(1+x2), then f is both one - one and onto when B, is the interval
View SolutionOne of the root equation cosx−x+12=0 lies in the interval (0,π2) (b) (−π2,0) (c) (π2,π) (d) (π,3π2)
View SolutionThe function f(x)=tan−1(sinx+cosx) is an increasing function in (−π2,π4) (b) (0,π2) (−π2,π2) (d) (π4,π2)
View SolutionRange of tan−1(2x1+x2) is (a)[−π4,π4] (b) (−π2,π2) (c)(−π2,π4) (d) [π4,π2]
View Solution1.The inverse of cosine function is defined in the intervals (A) [ −π,0]
(B) [ −π2,0] (C) [0,π2] (D) [ π2,π]
View SolutionOne root of the equation cosx−x+12=0 lies in the interval (A) [0,π2] (B) [−π2,0] (C) [π2,0] (D) none
View SolutionLet f:R→[0,π2) be defined by f(x)=tan−1(3x2+6x+a). If f(x) is an onto function . then the value of a si
View SolutionShow that f(x)=tan−1(sinx+cosx) is a decreasing function on the interval on (π/4, π/2) .
View SolutionLet f:[π,3π/2]→R be a function given by f(x)=[sinx]+[1+sinx]+[2+sinx]
Then , the range of f(x) is
View Solution
