If xyz=abc, then the least value of bcx+cay+abz, is
3abc
6abc
abc
4abc
The correct Answer is:A
To find the least value of bcx+cay+abz given that xyz=abc, we can apply the Arithmetic Mean-Geometric Mean (AM-GM) inequality.
1. Identify the Expression: We need to minimize the expression S=bcx+cay+abz.
2. Apply AM-GM Inequality: According to the AM-GM inequality, for any non-negative real numbers u,v,w:
u+v+w3≥√(3)uvw
We can apply this to our terms bcx, cay, and abz.
3. Set Up the Inequality:
bcx+cay+abz3≥√(3)(bcx)(cay)(abz)
4. Calculate the Product:
(bcx)(cay)(abz)=b2c2a2xyz
Since we know xyz=abc, we can substitute:
(bcx)(cay)(abz)=b2c2a2(abc)=a3b3c3
5. Substitute Back into the Inequality:
bcx+cay+abz3≥√(3)a3b3c3=abc
6. Multiply Both Sides by 3:
bcx+cay+abz≥3abc
7. Conclusion: The least value of bcx+cay+abz is 3abc.
Final Answer:
The least value of bcx+cay+abz is 3abc.
---
u+v+w3≥√(3)uvw
We can apply this to our terms bcx, cay, and abz.
bcx+cay+abz3≥√(3)(bcx)(cay)(abz)
(bcx)(cay)(abz)=b2c2a2xyz
Since we know xyz=abc, we can substitute:
(bcx)(cay)(abz)=b2c2a2(abc)=a3b3c3
bcx+cay+abz3≥√(3)a3b3c3=abc
bcx+cay+abz≥3abc
The least value of bcx+cay+abz is 3abc.
Topper's Solved these Questions
- INEQUALITIES BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - Section II - Assertion Reason Type
1 Videos
- INEQUALITIES BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - EXERCISE SECTION-II (Assertion-Reason )
1 Videos
- INEQUALITIES BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - Section 2 - Assertion Reason Type
9 Videos
- HYPERBOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - HYPERBOLAEXERCISE - Chapter Test
29 Videos
- LOGARITHMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LOGARITHMSEXERCISE - Chapter Test
21 Videos
Similar Questions
Knowledge Check
The least value of cos2x+sec2x is :
A1B0C−1D2If xy=2,xz=8andyz=5, then the value of xyz is closest to:
A5B9C15D25
The denominator of a fraction exceeds the square of the numberator by 16, then the least value of the fraction is
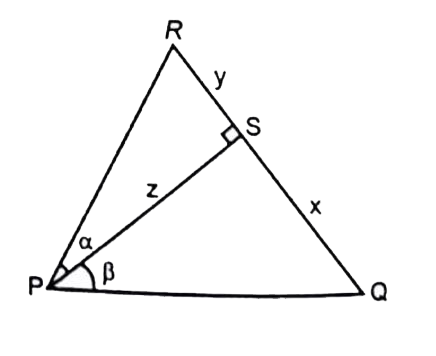
View SolutionIn a ΔPQR (as shown in figure) if x:y:z=2:3:6, then the value of ∠QPR is :
View SolutionThe least values of cosec2x+25sec2x is
View SolutionThe least value of f(x)=x33−abx occurs at x=
View SolutionThe least value of 5sinx−1+5−sinx−1, is
View SolutionIf a, b, c are three distinct positive real numbers, then the least value of
(1+a+a2)(1+b+b2)(1+c+c2)abc, is
View Solution
