The sum ∑0≤i∑≤j≤10(10Cj)(jCi) is equal to
210−1
210
310−1
310
The correct Answer is:C
To solve the problem, we need to evaluate the double summation:
j∑i=010∑j=0(10j)(ji)
Step 1: Understand the summation
We have a double summation where j varies from 0 to 10, and for each j, i varies from 0 to j. The terms involved are binomial coefficients.
Step 2: Change the order of summation
We can rewrite the double summation by changing the order of summation. This means we will first sum over j and then over i:
10∑j=0(10j)j∑i=0(ji)
Step 3: Evaluate the inner summation
The inner summation j∑i=0(ji) represents the sum of the binomial coefficients for a fixed j. According to the binomial theorem, this sum equals 2j:
j∑i=0(ji)=2j
Step 4: Substitute back into the outer summation
Now we substitute this result back into the outer summation:
10∑j=0(10j)2j
Step 5: Recognize the outer summation as a binomial expansion
The expression 10∑j=0(10j)2j can be recognized as the expansion of (2+1)10 using the binomial theorem:
n∑j=0(nj)xj=(x+1)n
Here, n=10 and x=2:
10∑j=0(10j)2j=(2+1)10=310
Step 6: Final result
Thus, the value of the original double summation is:
310
Conclusion
The final answer is 310.
---
Topper's Solved these Questions
Similar Questions
The sum ∑∑0≤i≤j≤10(10Cj)(jCr−1) is equal to
View SolutionThe value of ∑0≤i<j≤5∑(5Cj)(jCi) is equal to _____
View SolutionStatement1: ∑∑0≤i<j≤n(i.nci+j.ncj) is equal ton22a , where a ,n∑r=01.ncr=a Statement2:n∑r=0r.ncr=n∑r=0n−r.ncr
View SolutionLatA=[aij]3×3. If tr is arithmetic mean of elements of rth row and aij+ajk+aki=0 holde for all 1≤i,j,k≤3. ∑1≤i∑j≤3aij is not equal to
View SolutionEvaluate ∑0≤i≤j≤1021Ci⋅21Cj.
View SolutionThe value of n∑r=0r∑p=0nCr.rCp is equal to
View SolutionFind the sum 10∑j=110∑i=1i×2j
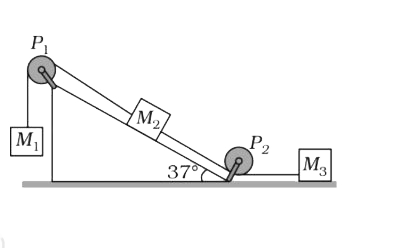
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View Solutionn∑i=1n∑i=1i is equal to
View SolutionFind the sum ∑∑0≤i<j≤n−1jnCt
View Solution
