Let x=33n . The index n is given a positive integral value at random. The probability that the value of x will have 3 in the units place is
13
14
15
12
The correct Answer is:B
We have,
31=3,32=9,33=27,34=81,35=243,36=729 etc.
So, a natural number of the form 3n may have either 3 or 9 or 7 or 1 at unit's place.
∴ Total number of elementary events=4
Clearly, only one number has 3 at unit's place.
∴ Favourable number of ways=1
Hence, required probability=14
Topper's Solved these Questions
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)
15 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Section I - Mcqs
89 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
Similar Questions
If n is a positive integer then the probability that 3n has 3 at unit place is
View SolutionThere are n letters and n addressed envelopes . If the letters are placed in the envelopes at random , what is the probability that all the letters are not placed in the right evelope ?
View SolutionFor how many positive integral values of n does n! end with precisely 25 zeros?
View SolutionThe smallest positive integral value of n for which (1+√3i)n2 is real is
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionThe probability of a random variable X is given below
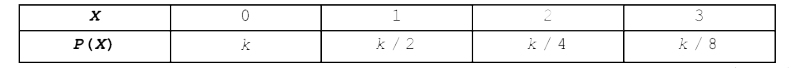
Determine the value of k
View SolutionThe least integral value of x for which 33−x(2+3x)>0 is
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View Solution
