Question

Let $0<\alpha <\frac{\pi }{2}$ be a fixed angle. If $P=(\cos \theta ,\sin \theta )\text{and}Q=(\cos (\alpha -\theta ),\sin (\alpha -\theta ),$ then Q is obtanied from P by

Options

A. clockwise rotation around origin through an angle `alpha`
B. anti-clockwise rotation around origin through an angle `alpha`
C. reflection in the line through origin with slope tan `alpha`
D. reflection in the line through origin with slope tan `alpha//2`

Answer

D

Explanation

We observe that the clockwise rotation of the point `P(costheta,sin theta))` and anticlockwise rotation through angle `alpha` takes P to the point `(cos(theta+alpha), sin(theta+alpha))`
Thus, option, (a) and (b) are not correct

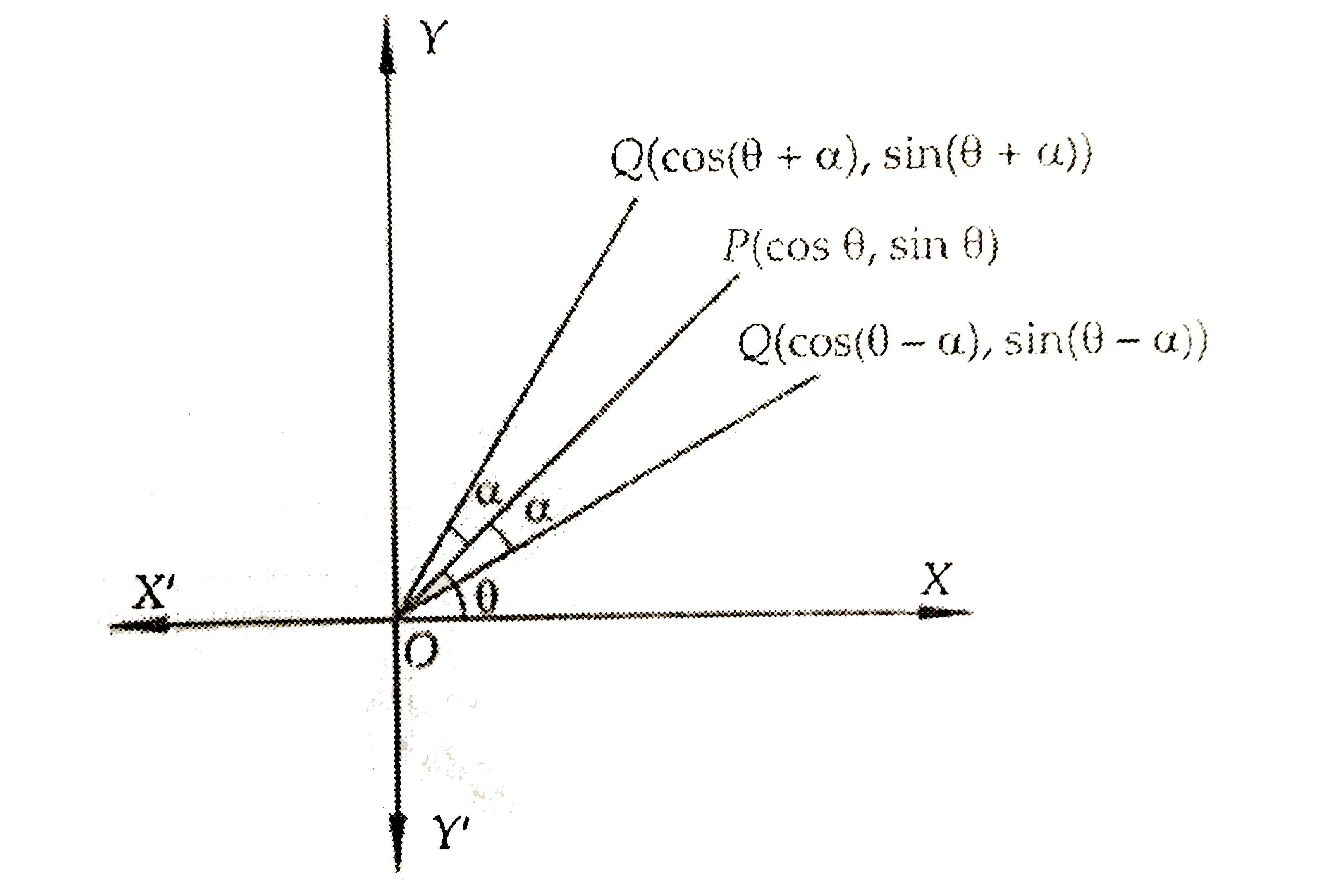
Now,
Slope of PQ`=(sin (alpha-theta)-sin theta)/(cos(alpha-theta)-costheta)`
`implies` Slope of PQ `=(2sin((alpha)/(2)-theta)"cos"(alpha)/(2))/(2sin ((alpha)/(2)-theta)"sin"(alpha)/(2))=-"cot"(alpha)/(2)`
This shows that PQ is perpendicular to a line with slope tan `alpha//2` . Thus, Q can be obtained from P by taking its reflection in the line with slope tan `alpha//2`.