Let A and B have coordinates (x1,y1) and (x2,y2) respectively . We define the distance between A and B as
d (A , B) = max {|x2−x1|,|y2−y1|}
If d ( A, O) = 1 , where O is the origin , then the locus of A has an area of
1sq. Unit
2 sq. units
4sq. units
1/4 sq. units
The correct Answer is:C
Let the coordinates of A be (h ,k) . Then ,
d(A,O) = 1
⇒ max {|h| , |k|} = 1
⇒|h|≤1
⇒ Locus of A (h,k) is |x|≤1,|y|≤1
Clearly , |x|≤1 and |y|≤1 represent the region enclosed by the square shown in fig. 40 .
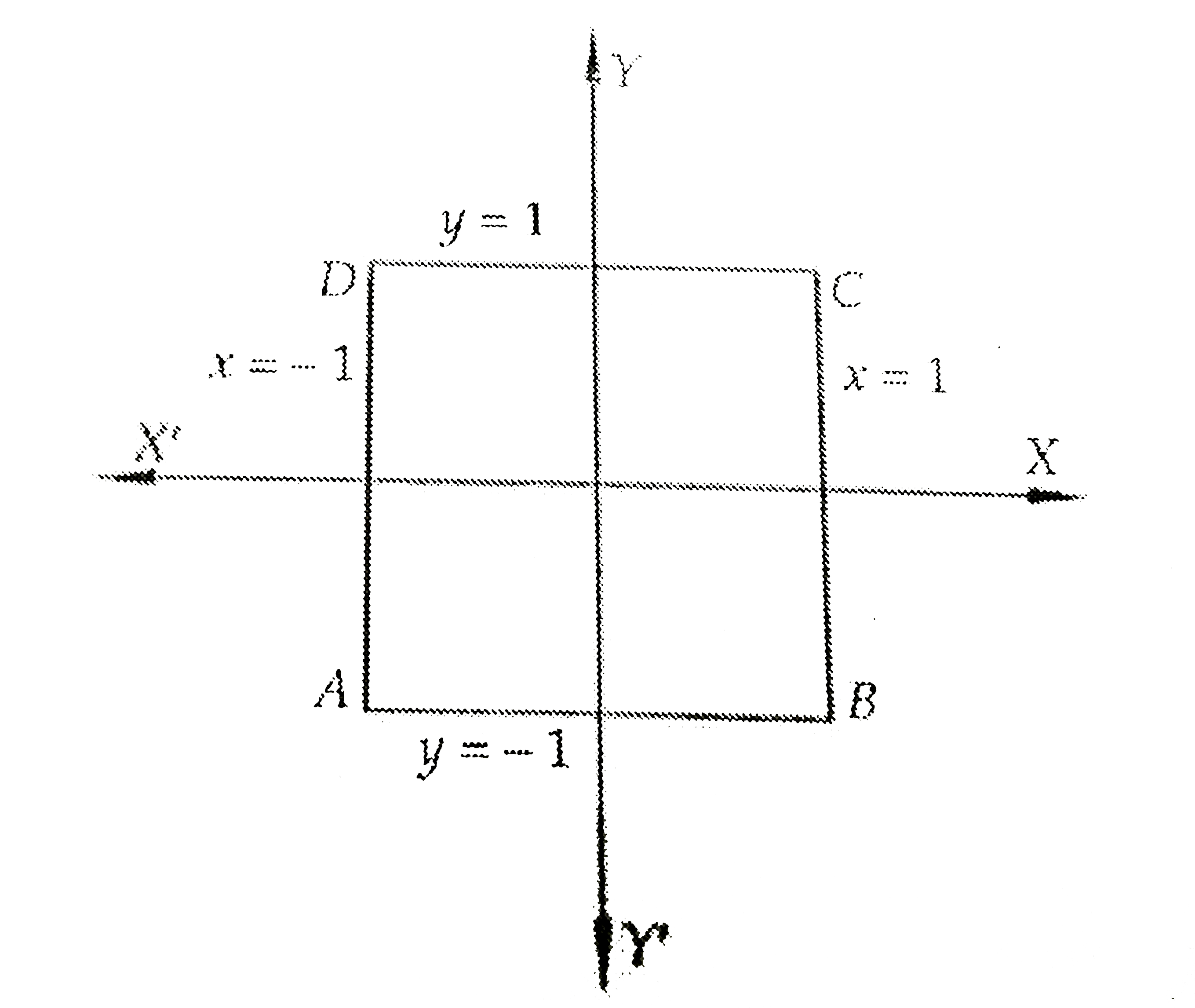
∴ Area enclosed by the locus of A = 2×2=4sq. units
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)1videos
STRAIGHT LINES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)14videos
STRAIGHT LINES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 181videos
STRAIGHT LINES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test30videos
SETS
Similar Questions
If O is the origin and P(x1,y1),Q(x2,y2) are two points then OPxOQsin∠POQ=
View SolutionFor points P≡(x1,y1)andQ=(x2,y2) of the coordinate plane , a new distance d (P,Q) is defined by d(P,Q) =|x1−x2|+|y1−y2|. Let O≡(0,0),A≡(1,2),B≡(2,3)andC≡(4,3) are four fixed points on x-y plane
Let S(x,y) such that S is equidistant from points O and B with respect to new distance and if x≥2and0≤y<3 then locus of S isView SolutionFor points P≡(x1,y1)andQ=(x2,y2) of the coordinate plane , a new distance d (P,Q) is defined by d(P,Q) =|x1−x2|+|y1−y2| Let O≡(0,0),A≡(1,2),B≡(2,3)andC≡(4,3) are four fixed points on x-y plane
Let R(x,y) such that R is equidistant from the point O and A with respect to new distance and if 0≤x<1and0≤y<2, then R lie on a line segment whose equation isView SolutionFor points P≡(x1,y1)andQ=(x2,y2) of the coordinate plane , a new distance d (P,Q) is defined by d(P,Q) =|x1−x2|+|y1−y2| Let O≡(0,0),A≡(1,2)B≡(2,3)andC≡(4,3) are four fixed points on x-y plane
Le T(x,y) such that T is equisdistant from point O and C with respect to new distance and if T lie in first quadrant , then T consists of the union of a line segment of finite length and an infinite ray whose labelled diagram isView SolutionIf A={x!,y1,z1} and B={x2,y2}, then the number of relations from A to B is
View SolutionProve that the line passing through the points (x1,y1) and (x2,y2) is at a distance of ∣∣ ∣ ∣∣x1y2−x2y1√(x2−x1)2+(y2−y1)2∣∣ ∣ ∣∣ from origin.
View SolutionIf the lines x=a1y+b1,z=c1y+d1 and x=a2y+b2,z=c2y+d2 are perpendicular, then
View SolutionLet A(x1,y1) and B(x2,y2) be two points on the parabola y2=4ax. If the circle with chord AB as a dimater touches the parabola, then |y1−y2| is equal to
View SolutionA path of length n is a sequence of points (x1,y1), (x2,y2),….,(xn,yn) with integer coordinates such that for all i between 1 and n−1 both inclusive,
either xi+1=xi+1 and yi+1=yi (in which case we say the ith step is rightward)
or xi+1=xi and yi+1=yi+1 ( in which case we say that the ith step is upward ).
This path is said to start at (x1,y1) and end at (xn,yn). Let P(a,b), for a and b non-negative integers, denotes the number of paths that start at (0,0) and end at (a,b).
Number of ordered pairs (i,j) where i≠j for which P(i,100−i)=P(i,100−j) isView SolutionIf A(x1,y1),B(x2,y2)andC(x3,y3) are vertices of an equilateral triangle whose each side is equal to a, then prove that
∣∣ ∣ ∣∣x1y12x2y22x3y32∣∣ ∣ ∣∣ is equal toView Solution

