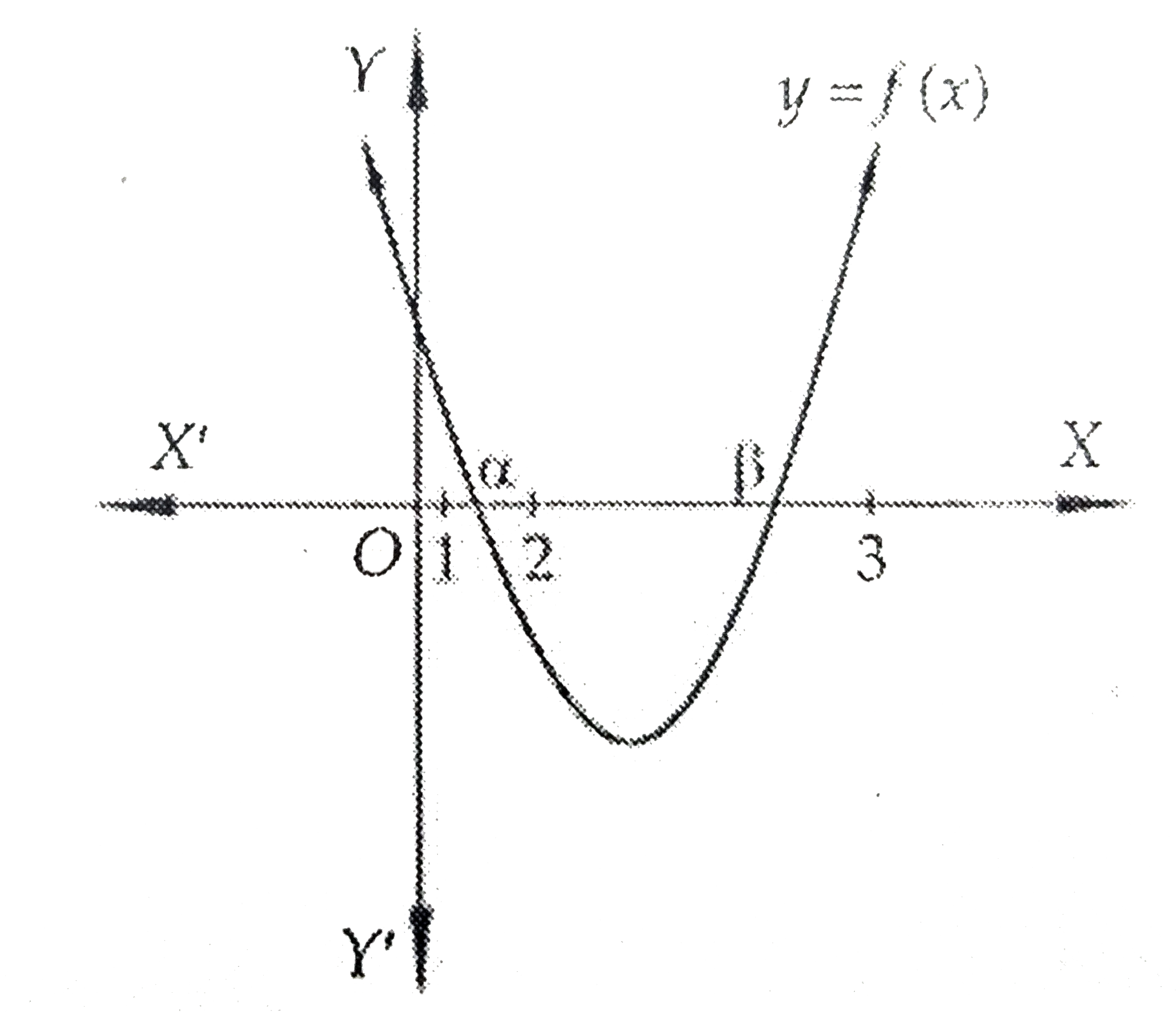
If α,β be the roots of the equation 4x2−16x+c=0,cεR such that 1<α<2 and 2<β<3, then the number of integral values of c are
5
6
2
3
The correct Answer is:D
Let f(x)=4x2−16x+c.
Clearly, 1 and 3 lie outside the roots and 2 lies between the roots.
∴ f(1)>0,f(2)<0andf(3)>0
⇒ c−12>0andc−16<0⇒12<c<16⇒c=13,14,15
Topper's Solved these Questions
- QUADRATIC EXPRESSIONS AND EQUATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:QUADRATIC EXPRESSIONS AND EQUATIONS Exercise:Section II - Assertion Reason Type
Explore 22 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:QUADRATIC EXPRESSIONS AND EQUATIONS Exercise:Exercise
Explore 138 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:QUADRATIC EXPRESSIONS AND EQUATIONS Exercise:Chapter Test
Explore 50 Videos
- PROBABILITY Book:OBJECTIVE RD SHARMA ENGLISHChapter:PROBABILITY Exercise:Chapter Test
Explore 45 Videos
- SEQUENCES AND SERIESBook:OBJECTIVE RD SHARMA ENGLISHChapter:SEQUENCES AND SERIESExercise:Chapter Test
Explore 59 Videos
Similar Questions
If α,β be the roots of 4x8−16x+c=0,c∈R such that 1<α<2and2<β<3, then the number of integral values of c is
View SolutionIf α,β be the roots of 4x2−17x+λ=0,λ∈R such that 1<α<2 and 2<β<3 then the number of integral values of λ is
View SolutionIf αandβ are the roots of the equation x2+αx+β=0 such that α≠β, then the number of integral values of x satisfying ||x−β|−α|<1 is
View SolutionIf α,β are the roots of the equation x2+αx+β=0 such that α≠β and ||x−β|−α|∣<α, then
View SolutionIf α,β(α<β) are the real roots of equation x2−(k+4)x+k2−12=0 such theta 4∈(α,β), then the number of integral value of k is equal to
View SolutionIf αandβ are the roots of the equation x2−px+16=0 , such that α2+β2=9, then the value of p is
View SolutionIf a<c<b then the roots of the equation (a−b)x2+2(a+b−2c)x+1=0 are
View SolutionIf α,β are the roots of the equation ax2+bx+c=0 then the value of (1+α+α2)(1+β+β2) is
View SolutionIf αandβ(α<β) are the roots of the equation x2+bx+c=0, where c<0<b, then
View SolutionIf c<a<b<d, then roots of the equation bx2+(1−b(c+d)x+bcd−a=0
View Solution
