The equation to the pair of straight lines bisecting the angles between the straight line
ax2+2hxy+by2=0
(a−b)(x2−y2)−4xy=0
(a−b)(x2+y2)+4hxy=0
(a−b)(x2−y2)+4xy=0
none of these
The correct Answer is:C
Step by step video solution for The equation to the pair of straight lines bisecting the angles between the straight line ax^(2) + 2hxy + by^(2) = 0 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PAIR OF STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise
34 Videos
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise
28 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
Similar Questions
Find the angle between the pair of straight lines x2−3xy+2y2=0
View SolutionThe lines y=mx bisects the angle between the lines ax2+2hxy+by2=0 if
View SolutionThe angle between the straight lines x2−y2−2x−1=0, is
View SolutionFindthe angle between the pair of straight lines x2−4y2+3xy=0
View SolutionThe equation of the straight line which bisects the intercepts between the axes of the lines x+y=2and 2x+3y=6 is
View SolutionThe angle between the straight lines 2x−y+3=0andx+2y+3=0 is-
View SolutionIf u≡ax2+2hxy+by2+2gx+2fy+c=0
represents a pair of straight lines , prove that the equation of the third pair of straight lines passing through the points where these meet the axes is ax^2 −2hxy+by 2 +2gx+2fy+c+ c 4fg xy=0.
View SolutionShow that the equation of the pair of lines bisecting the angles between the pair of bisectors of the angles between the pair of lines ax2+2hxy+by2=0 is (a−b)(x2−y2)+4hxy=0.
View SolutionShow that the equation of the pair of lines bisecting the angles between the pair of bisectors of the angles between the pair of lines ax2+2hxy+by2=0 is (a−b)(x2−y2)+4hxy=0.
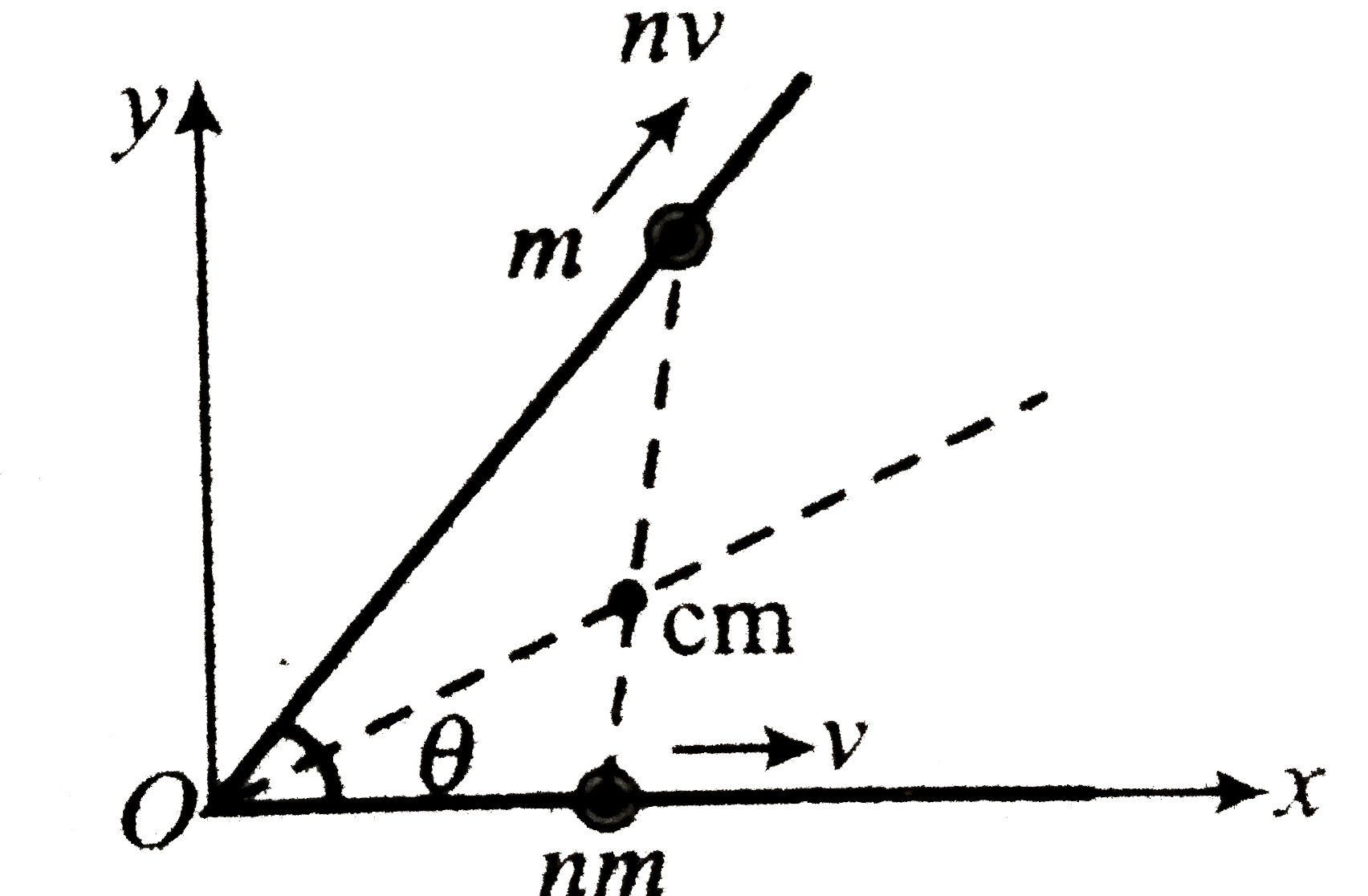
View SolutionTwo masses nm and m, start simultaneously from the intersection of two straight lines with velocities v and nv respectively. It is observed that the path of their centre of mass is a straight line bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here θ=angle between the lines]
View Solution
