Let $S$ be the area of the region enclosed by $y - e^{- x^{2}}, y = 0, x = 0$ and $x = 1$ . Then

A

$S \geq \frac{1}{e}$

B

$S \geq - \frac{1}{e}$

C

$S \leq \frac{1}{4} (1 + \frac{1}{\sqrt{e}})$

D

$S \leq \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{e}} (1 - \frac{1}{\sqrt{2}})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c

Clearly , $S = 1 \int 0 e^{- x^{2}} d x$

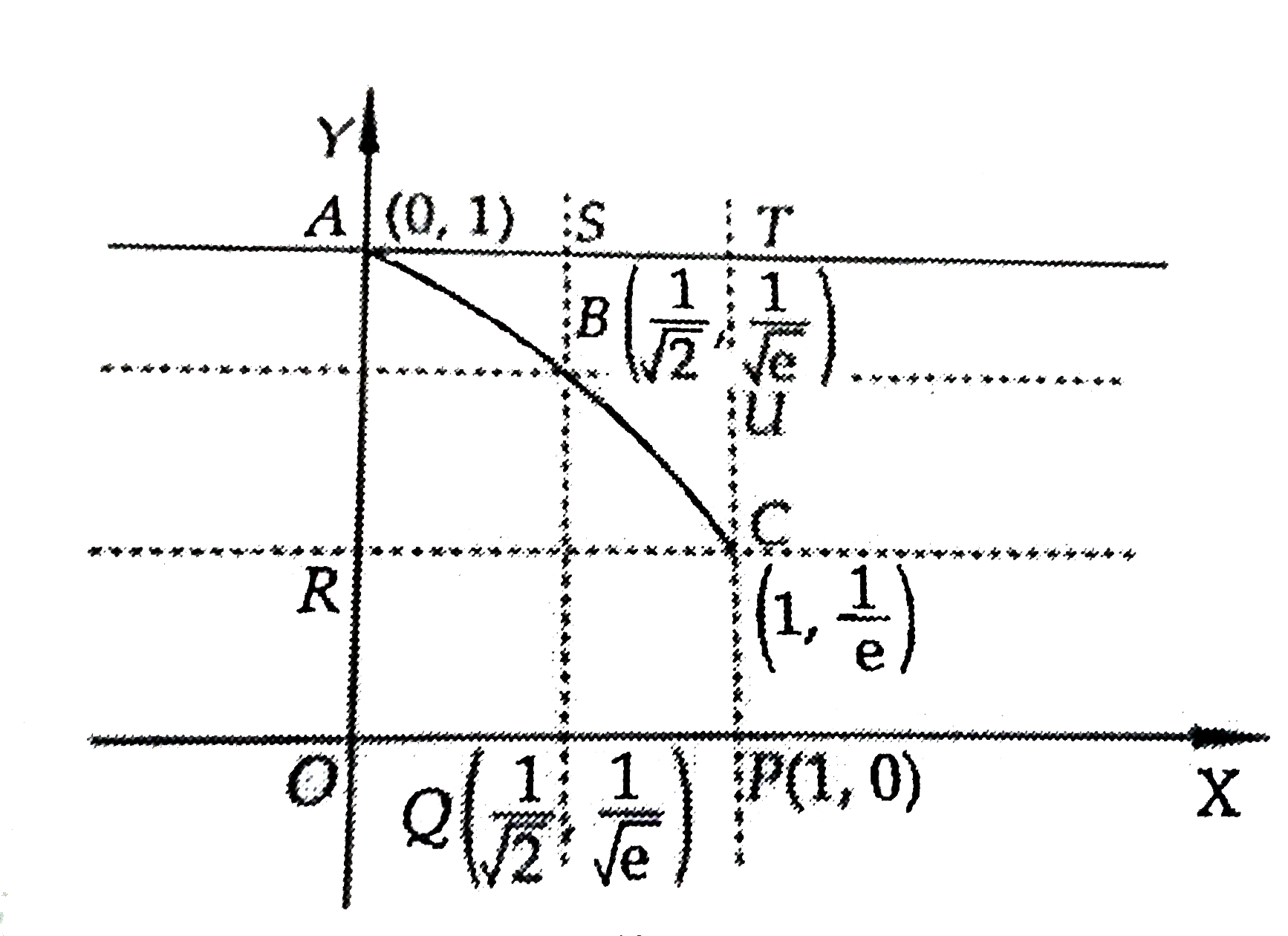
Also, $S >$ area of rectangle OPCR
$\Rightarrow S > O P \times O R \Rightarrow S > 1 \times \frac{1}{e} \Rightarrow S > \frac{1}{e}$
Now , $e^{- x^{2}} d x \geq e^{- x}$ for all $x \in [0, 1]$
$\Rightarrow {1 e 0}^{- x^{2}} d x > {1 e 0}^{- x} d x$
$\Rightarrow S \geq {[- e^{- x}]}_{0}^{- x} \Rightarrow S \geq (- \frac{1}{e} + 1) \Rightarrow S \geq 1 - \frac{1}{e}$
Clearly, $S <$ Area of rectangle OASQ + Area of rectangle PQBU
$\Rightarrow S \leq \frac{1}{\sqrt{2}} \times 1 + (1 - \frac{1}{\sqrt{2}}) \frac{1}{\sqrt{e}} = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{e}} (1 - \frac{1}{\sqrt{2}})$
Since $\frac{1}{4} (1 + \frac{1}{\sqrt{e}}) < 1 - \frac{1}{e} .$ Therefore , $S > \frac{1}{4} (1 + \frac{1}{\sqrt{e}})$ .

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

OBJECTIVE RD SHARMA ENGLISH-AREAS OF BOUNDED REGIONS-Chapter Test

Home
Ask Doubt
Profile