Area of the region
{(x,y)∈R2:y≥√|x+3|,5y≤x+9≤15} is equal to

A

16

B

43

C

32

D

53

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:c

We have, y≥√|x+3|
⇒y2≥|x+3|
⇒y2≥(x+3) for x≥−3andy2≥−(x+3) for x<−3
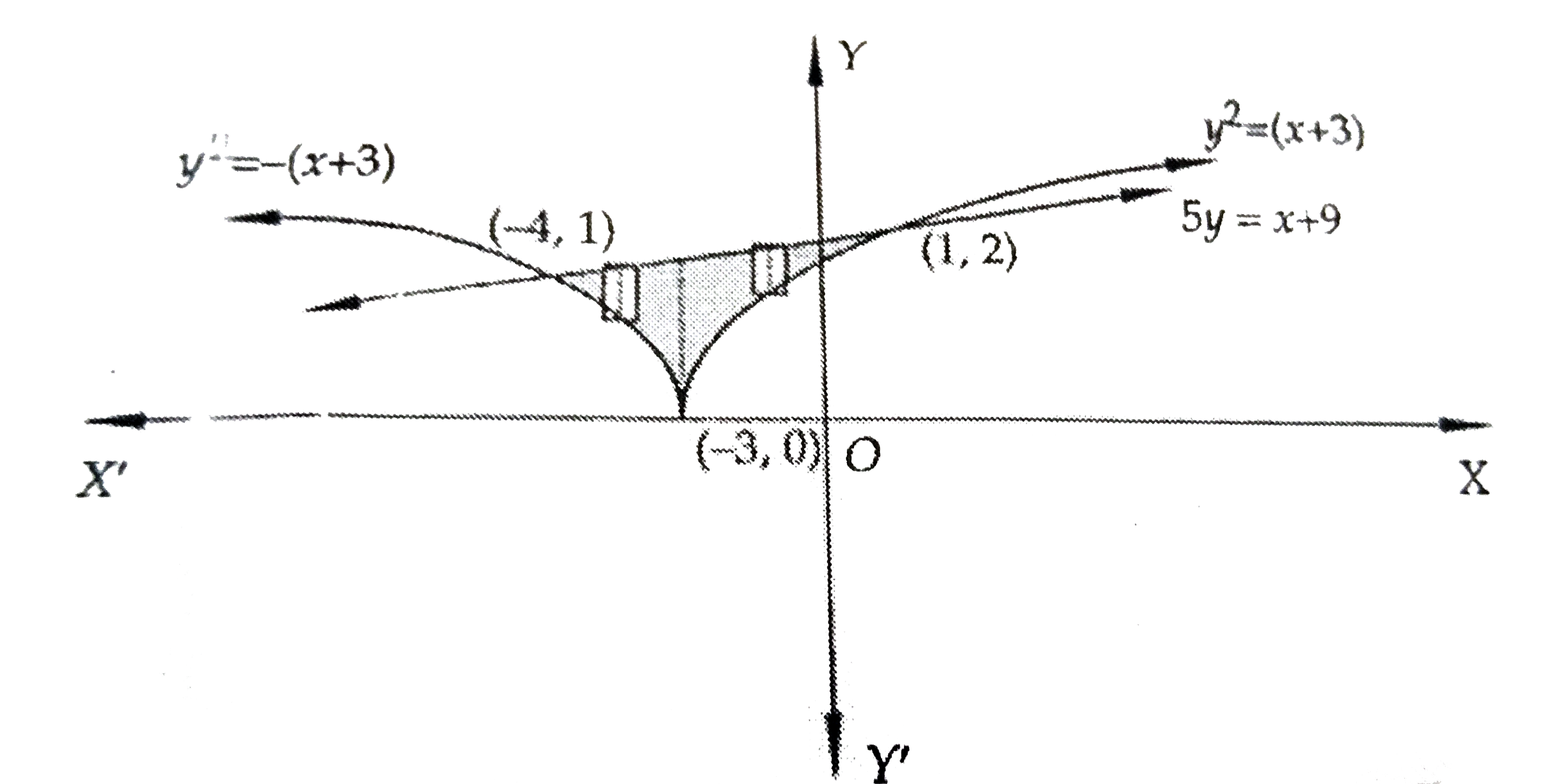
ocr_image
Required area A is given by
A=−3∫−4(x+95−√−x−3)dx+1∫−3(x+95−√x+3)dx
⇒A=15−1∫−4(x+9)dx−−3∫−4√−4−3dx−−1∫−3√x+3dx
⇒A=[15(x+9)22]1−4+23[(−x−3)3/2]−3−4−23[(x+3)3/2]1−3
⇒A=15(50−252)+23(0−1)−23(8−0)=32

Updated on:21/07/2023
|