If the tangent at a point on the ellipse meets the coordinate axes at and and the origin, then the minimum area (in sq. units) of the triangle is:
9
The correct Answer is:A
Let be a point on the ellipse. Then, the equation of the tangent at P is
.
This meets the coordinate axes at .
Let be the area of Then,
Clearly, is minimum when is maximum. The maximum value of is 1. Hence, the minimum value of is 9.
Topper's Solved these Questions
- TANGENTS AND NORMALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:TANGENTS AND NORMALSExercise:Section I - Solved Mcqs
Explore 49 Videos
- TANGENTS AND NORMALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:TANGENTS AND NORMALSExercise:Exercise
Explore 42 Videos
- SOLUTIONS OF TRIANGLES Book:OBJECTIVE RD SHARMA ENGLISHChapter:SOLUTIONS OF TRIANGLES Exercise:Exercise
Explore 20 Videos
- THREE DIMENSIONAL COORDINATE SYSTEM Book:OBJECTIVE RD SHARMA ENGLISHChapter:THREE DIMENSIONAL COORDINATE SYSTEM Exercise:Exercise
Explore 20 Videos
Similar Questions
The tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionTangent at a point on the ellipse x2a2+y2b2=1
is drawn which cuts the coordinates axes at A and B the minimum area of the triangle OAB is ( O being origin )
View SolutionIf any tangent to the ellipse 25x2+9y2=225 meets the coordinate axes at A and B such that OA = OB then , the length AB is equal to (where , O is the origin)
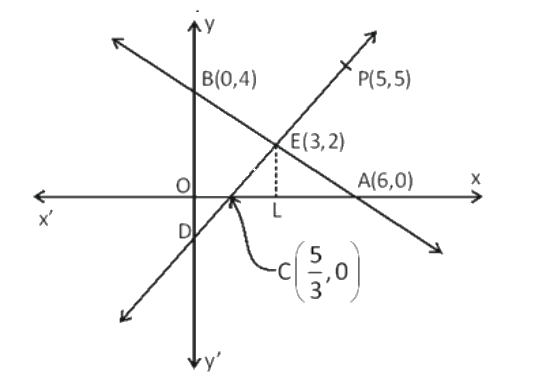
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionTangents are drawn to the hyperbola 4x2−y2=36 at the points P and Q. If these tangents intersect at the point T(0,3) then the area (in sq units) of △PTQ is
View SolutionTangents are drawn to the hyperbola 4x2−y2=36 at the points P and Q. If these tangents intersect at the point T(0,3) then the area (in sq units) of △PTQ is
View SolutionIf a tangent having a slope of −43 to the ellipse x218+y232=1 intersects the major and minor axes in points AandB respectively, then the area of ΔOAB is equal to (A) 12 sq. untis (B) 24 sq. units (C) 48 sq. units (D) 64 sq. units
View Solutiontangent drawn to the ellipse x2a2+y2b2=1 at point 'P' meets the coordinate axes at points A and B respectively.Locus of mid-point of segment AB is
View SolutionIf the plane x2+y3+z4=1 cuts the coordinate axes in A,B,C, then the area of triangle ABC is
View Solution