If f(x) is a real valued odd function , then which one of the following is incorrect ?
f(x)−f(−x)2 is an odd function.
f(x)+f(−x)2 is an even function.
[|f(x)|+2] is an even function, [⋅] denotes the greatest integer function.
f(x)−f(−x)2 is neither even nor odd.
The correct Answer is:D
To determine which statement is incorrect given that f(x) is a real-valued odd function, we will analyze the properties of odd functions and evaluate the provided options.
1. Understanding Odd Functions:
An odd function satisfies the property:
f(−x)=−f(x)
for all x.
2. Evaluate Each Option:
We will analyze each option to see if it adheres to the properties of odd functions.
Option 1: Let g(x)=f(x)−f(−x).
- Using the property of odd functions:
g(x)=f(x)−(−f(x))=f(x)+f(x)=2f(x)
- Now, check if g(−x)=−g(x):
g(−x)=f(−x)−f(x)=−f(x)−f(x)=−2f(x)=−g(x)
- Therefore, g(x) is also an odd function.
Option 2: Let g(x)=f(x)+f(−x).
- Using the property of odd functions:
g(x)=f(x)+(−f(x))=0
- The function g(x)=0 is both even and odd.
Option 3: Let g(x)=greatest integer(|f(x)|)+2.
- Check g(−x):
g(−x)=greatest integer(|f(−x)|)+2=greatest integer(|−f(x)|)+2=greatest integer(|f(x)|)+2=g(x)
- Thus, g(x) is an even function.
Option 4: This option states that g(x) is neither even nor odd.
- Since we have established that options 1, 2, and 3 are correct, option 4 must be incorrect.
3. Conclusion:
The incorrect statement is Option 4.
An odd function satisfies the property:
f(−x)=−f(x)
for all x.
We will analyze each option to see if it adheres to the properties of odd functions.
- Using the property of odd functions:
g(x)=f(x)−(−f(x))=f(x)+f(x)=2f(x)
- Now, check if g(−x)=−g(x):
g(−x)=f(−x)−f(x)=−f(x)−f(x)=−2f(x)=−g(x)
- Therefore, g(x) is also an odd function.
- Using the property of odd functions:
g(x)=f(x)+(−f(x))=0
- The function g(x)=0 is both even and odd.
- Check g(−x):
g(−x)=greatest integer(|f(−x)|)+2=greatest integer(|−f(x)|)+2=greatest integer(|f(x)|)+2=g(x)
- Thus, g(x) is an even function.
- Since we have established that options 1, 2, and 3 are correct, option 4 must be incorrect.
The incorrect statement is Option 4.
Topper's Solved these Questions
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Section I - Solved Mcqs
95 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type
8 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
63 Videos
Similar Questions
Knowledge Check
If |x|+x=4, then which one of the following is odd?
Ax2+3xBx2+3x+2Cx2+4xDx2+4x+3A function f(x) is defined as even if and only if f(x)=f(−x) for all real values of x. Which one of the following graphs represents an even function f(x) ?
A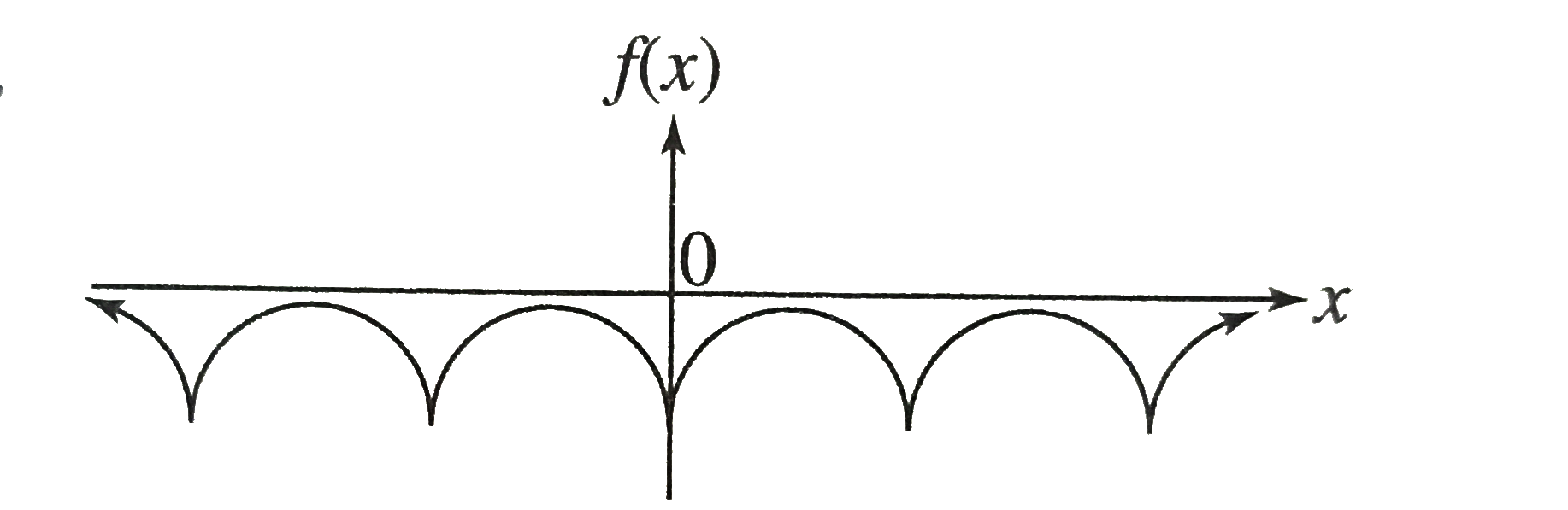 B
B C
C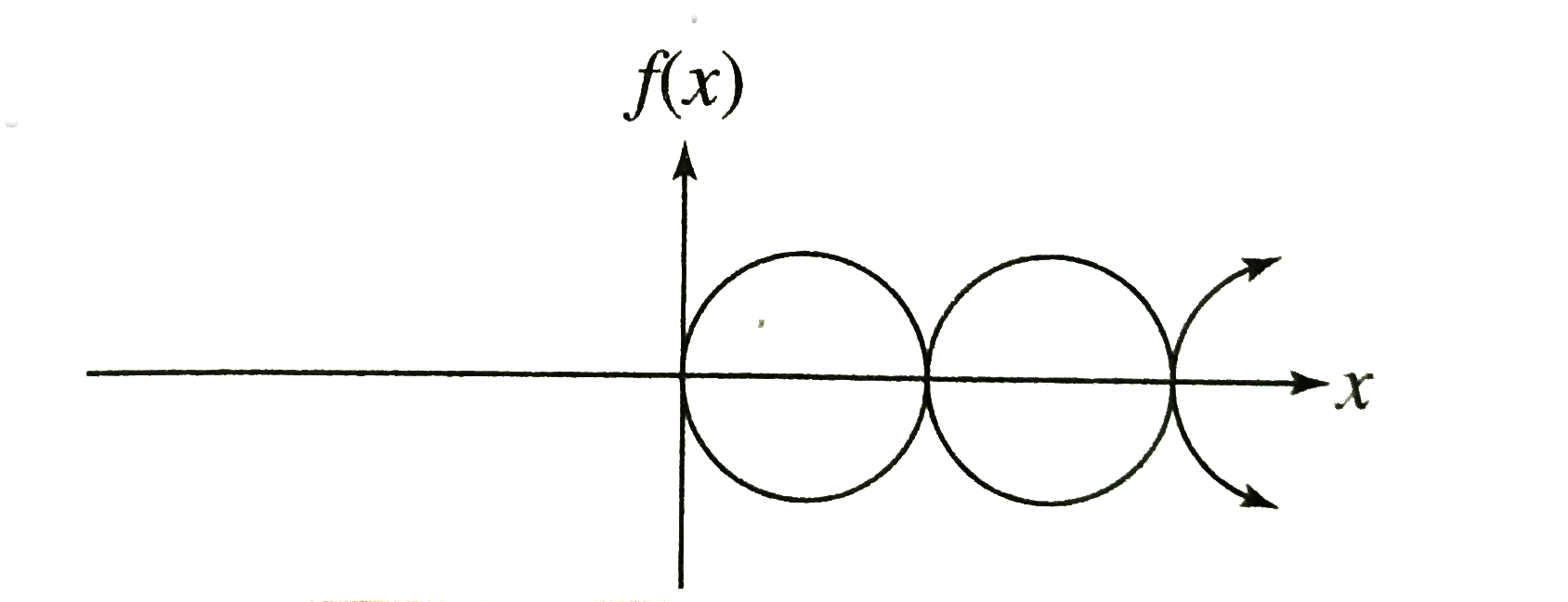 D
D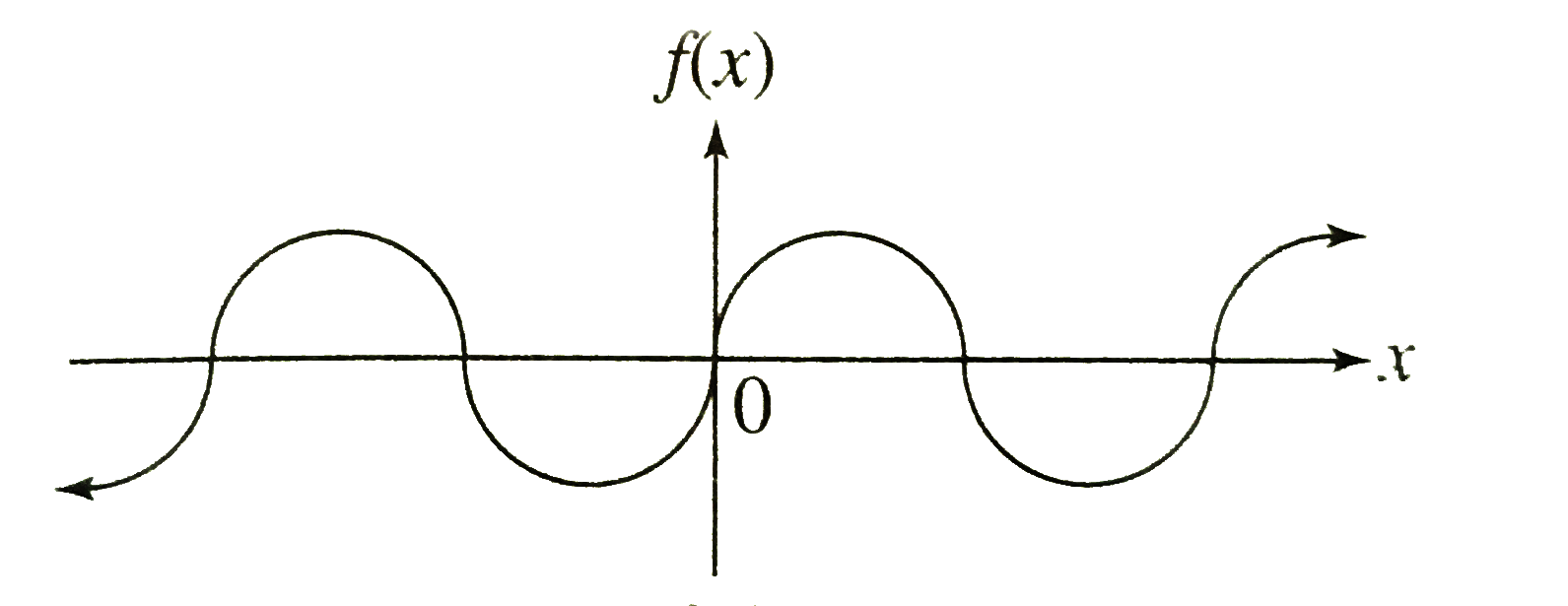
The table shows the values of the quadratic functions f for several values of x. Which one of the following best represents f?
x−101 2f(x) 131−5Af(x)=−2x2Bf(x)=x2+3Cf(x)=−x2+3Df(x)=−2x2+3
Which of the following is not an odd function ?
View SolutionIf f(x)=x2 is a real function, find the value of f(1).
View SolutionIf f(x) is an odd function, then the curve y=f(x) is symmetric
View SolutionLet G(x)=(1ax−1+12)F(x), where a is a positive real number not equal to 1 and f(x) is an odd function. Which of the following statements is true? (a)G(x) is an odd function (b)G(x)is an even function (c)G(x) is neither even nor odd function. (d)Whether G(x) is an odd or even function depends on the value of a
View SolutionLet G(x)=(1ax−1+12)F(x), where a is a positive real number not equal to 1 and f(x) is an odd function. Which of the following statements is true? G(x) is an odd function G(x)is an even function G(x) is neither even nor odd function. Whether G(x) is an odd or even function depends on the value of a
View Solution
