If f(x)=ax, which of the following equalities do not hold ? (i) f(x+2)−2f(x+1)+f(x)=(a−1)2f(x) (ii) f(−x)f(x)−1=0 (iii) f(x+y)=f(x)f(y) (iv) f(x+3)−2f(x+2)+f(x+1)=(a−2)2f(x+1)
f(x+2)−2f(x+1)+f(x)=(a−1)2f(x)
f(−x)f(x)+1=0
f(x+y)=f(x)+f(y)
f(x+3)−2f(x+2)+f(x+1)=(a−2)2f(x+1)
The correct Answer is:A
To determine which of the given equalities do not hold for the function f(x)=ax, we will evaluate each equality step by step.
Step 1: Evaluate the first equality
Equality (i):
f(x+2)−2f(x+1)+f(x)=(a−1)2f(x)
Left-hand side:
f(x+2)=ax+2=a2ax
f(x+1)=ax+1=aax
f(x)=ax
Now substituting these into the left-hand side:
a2ax−2(aax)+ax=ax(a2−2a+1)
Factoring the quadratic:
ax((a−1)2)=(a−1)2f(x)
Conclusion: The first equality holds true.
Step 2: Evaluate the second equality
Equality (ii):
f(−x)f(x)−1=0
Left-hand side:
f(−x)=a−x=1ax
Now substituting into the left-hand side:
f(−x)f(x)=(1ax)(ax)=1
Thus:
1−1=0
Conclusion: The second equality holds true.
Step 3: Evaluate the third equality
Equality (iii):
f(x+y)=f(x)f(y)
Left-hand side:
f(x+y)=ax+y
Right-hand side:
f(x)f(y)=axay=ax+y
Conclusion: The third equality holds true.
Step 4: Evaluate the fourth equality
Equality (iv):
f(x+3)−2f(x+2)+f(x+1)=(a−2)2f(x+1)
Left-hand side:
f(x+3)=ax+3=a3ax
f(x+2)=ax+2=a2ax
f(x+1)=ax+1=aax
Now substituting these into the left-hand side:
a3ax−2(a2ax)+(aax)=ax(a3−2a2+a)
Factoring out ax:
=ax(a3−2a2+a)=ax(a2(a−2)+a)=ax(a2−2a+2)
Right-hand side:
(a−2)2f(x+1)=(a−2)2(aax)=ax(a−2)2a
Now, we need to check if:
ax(a3−2a2+a)=ax(a−2)2a
This simplifies to:
a3−2a2+a=(a−2)2a
Expanding the right-hand side:
=a(a2−4a+4)=a3−4a2+4a
Setting the two sides equal:
a3−2a2+a=a3−4a2+4a
Simplifying gives:
2a2−3a=0
Factoring out a:
a(2a−3)=0
This holds true only for a=0 or a=32, thus it does not hold for all a.
Conclusion
The equality that does not hold for all values of a is:
(iv) f(x+3)−2f(x+2)+f(x+1)=(a−2)2f(x+1)
Equality (i):
f(x+2)−2f(x+1)+f(x)=(a−1)2f(x)
f(x+2)=ax+2=a2ax
f(x+1)=ax+1=aax
f(x)=ax
Now substituting these into the left-hand side:
a2ax−2(aax)+ax=ax(a2−2a+1)
Factoring the quadratic:
ax((a−1)2)=(a−1)2f(x)
Conclusion: The first equality holds true.
Equality (ii):
f(−x)f(x)−1=0
f(−x)=a−x=1ax
Now substituting into the left-hand side:
f(−x)f(x)=(1ax)(ax)=1
Thus:
1−1=0
Conclusion: The second equality holds true.
Equality (iii):
f(x+y)=f(x)f(y)
f(x+y)=ax+y
Right-hand side:
f(x)f(y)=axay=ax+y
Conclusion: The third equality holds true.
Equality (iv):
f(x+3)−2f(x+2)+f(x+1)=(a−2)2f(x+1)
f(x+3)=ax+3=a3ax
f(x+2)=ax+2=a2ax
f(x+1)=ax+1=aax
Now substituting these into the left-hand side:
a3ax−2(a2ax)+(aax)=ax(a3−2a2+a)
Factoring out ax:
=ax(a3−2a2+a)=ax(a2(a−2)+a)=ax(a2−2a+2)
(a−2)2f(x+1)=(a−2)2(aax)=ax(a−2)2a
ax(a3−2a2+a)=ax(a−2)2a
This simplifies to:
a3−2a2+a=(a−2)2a
Expanding the right-hand side:
=a(a2−4a+4)=a3−4a2+4a
Setting the two sides equal:
a3−2a2+a=a3−4a2+4a
Simplifying gives:
2a2−3a=0
Factoring out a:
a(2a−3)=0
This holds true only for a=0 or a=32, thus it does not hold for all a.
The equality that does not hold for all values of a is:
(iv) f(x+3)−2f(x+2)+f(x+1)=(a−2)2f(x+1)
Topper's Solved these Questions
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type
8 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
63 Videos
Similar Questions
Knowledge Check
If (x)=ax−1ax+1 , choose the correct statement.
I. f(-x)=f(x)
II. F(-x)=-f(x)
III. F(2x)=2f(x)AOnly IBOnly IICOnly IIIDBoth II and III
Let f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)=|f(x)| (d) none of these
View SolutionIf f(x)=cos2x+sec2x, then
(i) f(x)<1
(ii) f(x)=1
(iii) 2<f(x)<1
(iv) f(x)≥2
View SolutionIf f(x)=log(1+x1−x),then (a)f(x1)f(x2)=f(x1+x2) (b)f(x+2)−2f(x+1)+f(x)=0 (c)f(x)+f(x+1)=f(x2+x) (d)f(x1)+f(x2)=f(x1+x21+x1x2)
View SolutionGiven the graph of y=f(x).
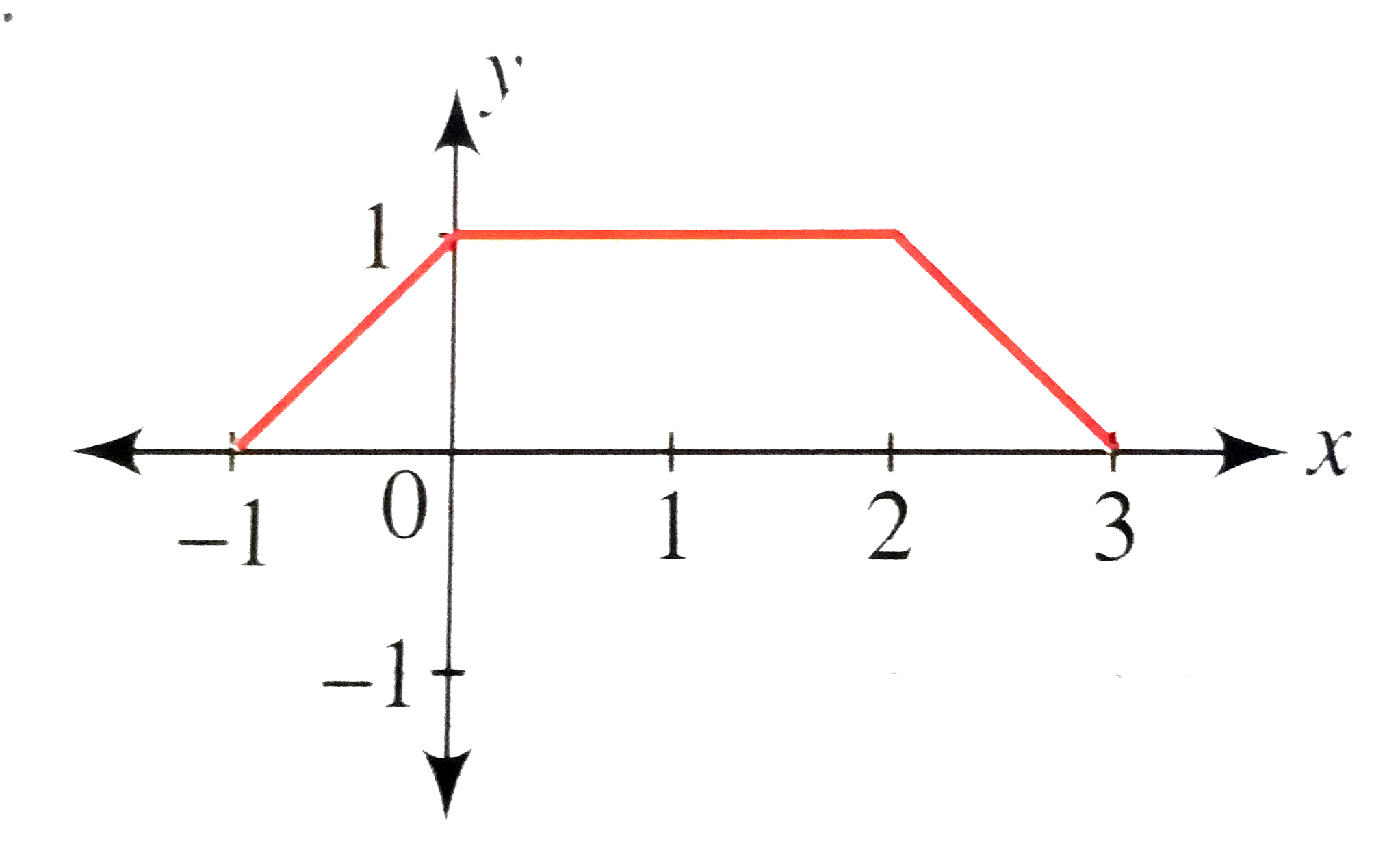
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View SolutionIf f(x)=x−1x+1 then f(2x) is equal to
View SolutionIf f(x)=x−1x+1 then f(2x) is equal to
View SolutionThe graph of y = f(x) is as shown in the following figure.

Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View Solution
