A transversal cuts the sides OL,OM and diagonal ON of a parallelogram at A,B and C respectively.
Prove that OLOA+OMOB=ONOC.
Statement - 1 is True, Statement - 2 is True , Statement - 2 is a correct explanation for Statement - 1.
Statement -1 is True, Statement - 2 is True, Statement -2 is not a correct explanation for Statement - 1.
Statement - 1 is True, Statement - 2 is False.
Statement - 1 is False, Statement - 2 is True.
The correct Answer is:A
statement -2 is true
Let −−→OL=x−−→OA,−−→OM=yO→Band−−→ON=z−−→OC. Then,
∣∣∣−−→OL∣∣∣=x∣∣∣−−→OA∣∣∣,∣∣∣−−→OM∣∣∣=y∣∣∣−−→OB∣∣∣and∣∣∣−−→ON∣∣∣=z∣∣∣−−→OC∣∣∣
⇒x=OLOA,y=OMOB,z=ONOC

Talking O as the origin, let the position vectors of A, B, C be →a,→band→c respectively.
In ΔOLN, we have
−−→OL+−−→LN=−−→ON
⇒−−→ON=−−→OL+−−→OM
⇒z−−→OC=x−−→OA+y−−→OB
⇒x−−→OA+y−−→OB−z−−→OC=→0⇒x→a+y→b+(−z)→c=→0
But, points A, B, C are collinear.
∴x→a+y→b+(−z)→c=→0
⇒x+y−z=0⇒x+y=z⇒OLOA+OMOB=ONOC
So, statement -1 is also true and statement -2 is a correct explanation for statement -1.
Topper's Solved these Questions
- ALGEBRA OF VECTORSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Exercise
30 Videos
- ALGEBRA OF VECTORSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRA OF VECTORSEXERCISE - Chapter Test
30 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
Similar Questions
Statement -1 : If a transversal cuts the sides OL, OM and diagonal ON of a parallelogram at A, B, C respectively, then
OLOA+OMOB=ONOC
Statement -2 : Three points with position vectors →a,→b,→c are collinear iff there exist scalars x, y, z not all zero such that x→a+y→b+z→c=→0, where x+y+z=0.
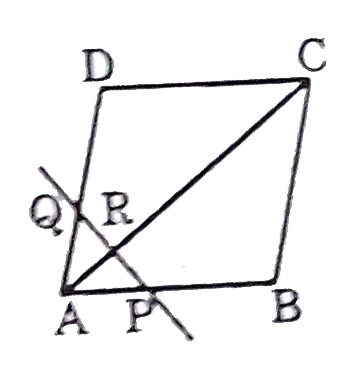
View SolutionA transversal cuts side AB and AD and diagonal AC of parallelogram ABCD in points P,Q and R respectively such that AP: PB =1 :2 and AQ: QD=2:3 . Find the ratio AR : RC
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionProve that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that :
(i) ADN≅CBP
(ii) AN=CP
View Solution
