Question

Two parallel chords of a circle, which are on the same side of centre,subtend angles of ${72}^{\circ }\text{and}{144}^{\circ }$ respetively at the centre Prove that the perpendicular distance between the chords is half the radius of the circle.

Options

A. 6
B. 4
C. 3
D. 2

Answer

A

Explanation

To prove that the perpendicular distance between two parallel chords of a circle, which subtend angles of $${72}^{\circ }$$ and $${144}^{\circ }$$ at the center, is half the radius of the circle, we will follow these steps:

Step 1: Draw the Circle and Chords
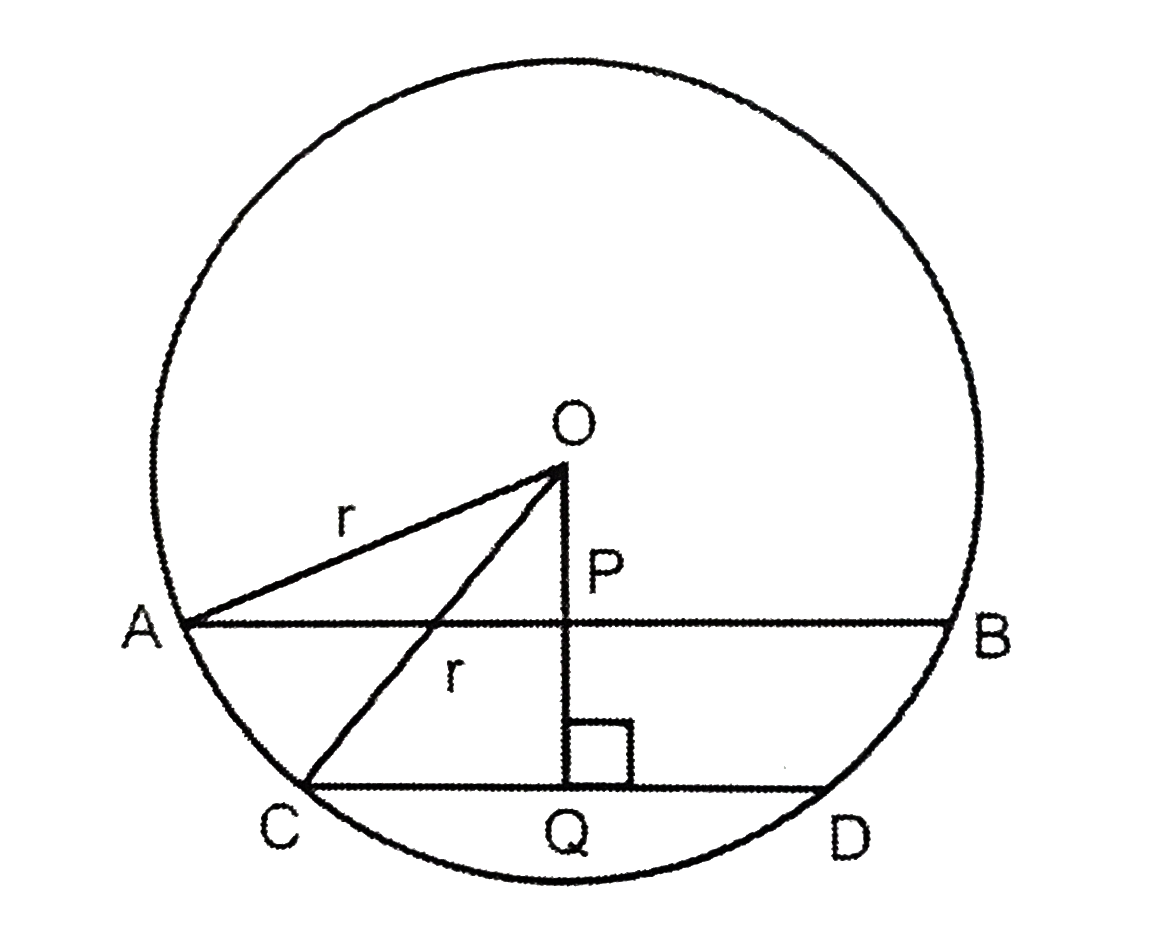
Let \(O\) be the center of the circle with radius \(r\). Draw two parallel chords \(AB\) and \(CD\) such that chord \(AB\) subtends an angle of \(72^\circ\) at the center \(O\) and chord \(CD\) subtends an angle of \(144^\circ\).

Step 2: Determine Angles in Triangles
Since \(AB\) subtends an angle of \(72^\circ\) at the center, the angles at the ends of the chord \(AB\) (i.e., \( \angle OAB\) and \( \angle OBA\)) can be calculated as follows:
\( \angle OAB = \angle OBA = \frac{180^\circ - 72^\circ}{2} = \frac{108^\circ}{2} = 54^\circ \)

Similarly, for chord \(CD\) which subtends an angle of \(144^\circ\):
\( \angle OCD = \angle ODC = \frac{180^\circ - 144^\circ}{2} = \frac{36^\circ}{2} = 18^\circ \)

Step 3: Use Sine Rule in Triangles
In triangle \(OAB\), using the sine definition:
\( \sin(54^\circ) = \frac{ON}{OA} \Rightarrow ON = r \sin(54^\circ) \)

In triangle \(OCD\):
\( \sin(18^\circ) = \frac{OM}{OC} \Rightarrow OM = r \sin(18^\circ) \)

Step 4: Calculate the Perpendicular Distance Between the Chords
The perpendicular distance \(MN\) between the two chords \(AB\) and \(CD\) is given by:
\( MN = ON - OM = r \sin(54^\circ) - r \sin(18^\circ) \)
Factoring out \(r\):
\( MN = r (\sin(54^\circ) - \sin(18^\circ)) \)

Step 5: Use Sine Values
Using known sine values:
\( \sin(54^\circ) = \frac{\sqrt{5} + 1}{4}, \quad \sin(18^\circ) = \frac{\sqrt{5} - 1}{4} \)
Substituting these values:
\( MN = r \left( \frac{\sqrt{5} + 1}{4} - \frac{\sqrt{5} - 1}{4} \right) \)
Simplifying:
\( MN = r \left( \frac{(\sqrt{5} + 1) - (\sqrt{5} - 1)}{4} \right) = r \left( \frac{2}{4} \right) = \frac{r}{2} \)

Conclusion
Thus, we have shown that the perpendicular distance \(MN\) between the two chords \(AB\) and \(CD\) is:
\( MN = \frac{r}{2} \)
This proves that the perpendicular distance between the chords is half the radius of the circle.