The projection of a line segment on the axis 2, 3, 6 respectively. Then find the length of line segment.
7
5
1
11
The correct Answer is:A
Let the length of the line segment be r and its direction cosines be l,m,n. Then its projections on the coordinate axes are lr,mr,nr.
∴lr=2,mr=3 and nr=6
⇒l2r2+m2r2+n2r2=4+9+36
⇒r2(l2+m2n2)=49
⇒r2=49⇒r=7[∵l2+m2+n2=1]
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Exercise
20 Videos
- THREE DIMENSIONAL COORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEM EXERCISE - Exercise
20 Videos
- TANGENTS AND NORMALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - TANGENTS AND NORMALSEXERCISE - Chapter Test
25 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Chapter Test
60 Videos
Similar Questions
The projection of a line segment on the axis 1, 2, 3 respectively. Then find the length of line segment.
View SolutionThe projections of a line segment on the coordinate axes are 12,4,3 respectively. The length and direction cosines of the line segment are
View SolutionSTATEMENT-1 : The distance of (3, 4, 5) from x-axis 5.
STATEMENT-2 : The distance of (x, y, z) from xy plane is z.
SATEMENT-3 : The projection of a line segment on the axes are 1, 2, 3 then the length of segment is √14
View SolutionThe length of a line segments can be measured.
View SolutionIs line a part of line segments ?
View SolutionIf the projection of a line segment of the x,y and z-axes in 3-dimensional space are 12,4, and 3 respectively, then the length of the line segmetn is (A) 13 (B) 9 (C) 6 (D) 7
View SolutionThe projection of a directed line segment on the coordinate axes are 12,4,3. Find its length and direction cosines.
View SolutionDraw a line segment of length 5.3cms
View SolutionThe projection of the line segment joining the points (1,−1,3) and (2,−4,11) on the line joining the points (−1,2,3) and (3,−2,10), is ……
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
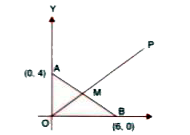
length of BP
View Solution
