A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are
A. y=2√3+x+1,y=−2√3x−1
B. y=1√3x,y=0
C. y=√32x+1,y=−√32x−1
D. y=√3x,y=0
(x−2√3)2+(y−1)2=1
(x−2√3)2+(y+12)2=1
(x−√3)2+(y+1)2=1
(x−√3)2+(y−1)2=1
The correct Answer is:D
Let A(h,k) be the centre of the circle. Then, AD⊥PQ and AD=1
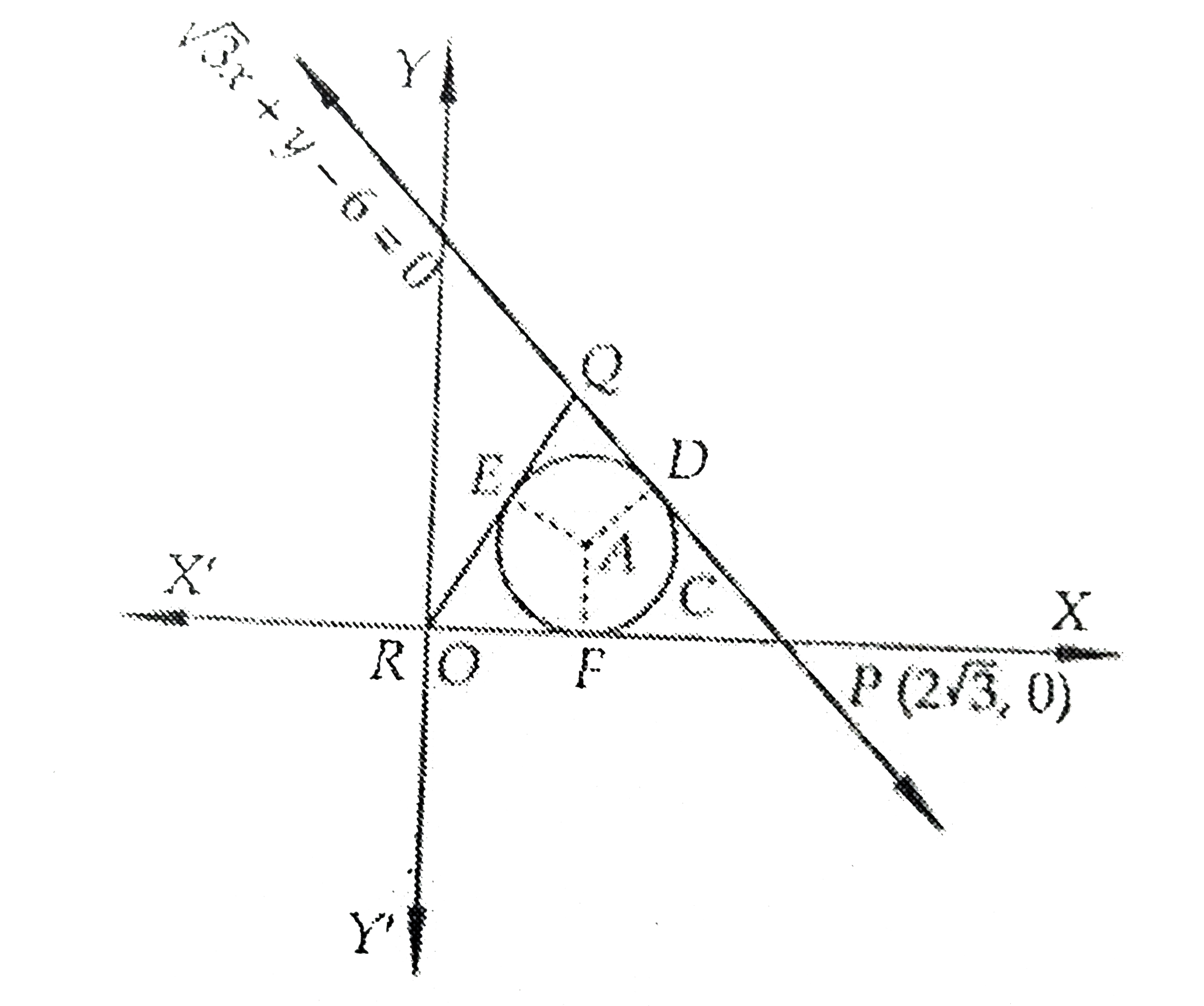
⇒2k−32h−3√3×(−√3)=−1and∣∣∣√3h+k−6√3+1∣∣∣=1
⇒2√3k−3√3=2h−3√3and∣∣√3h+k−6∣∣=2
⇒2h−2√3k=0and√3h+k−6=2or√3h+k−6=−2
⇒h=√3kand√3h+k−6=−2
[∴( Origin and (h, k) lie on the same side of √3x+y−6=0),(.∴√3h+k−6<0)]
⇒h=√3kand√3h+k=4
⇒h=√3,k=1
Hence, the equation of circle C is (x−√3)2+(y−1)2=1
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Video
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (3√32,32) The equation of circle C is : (A) (x−2√3)2+(y−1)2=1 (B) (x−2√3)2+(y+12)2=1 (C) (x−√3)2+(y+1)2=1 (D)(x−√3)2+(y−1)2=1
View SolutionThe vertex P of an equilateral triangle △PQR is at (2,3) and the equation of the opposite side QR is given by x+y=2. Find the possible equations of the side PQ.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionThe area of a circle inscribed in an equilateral triangle is 154 cm2 . Find the perimeter of the triangle. [Use π=22/7and √3=1.73]
View SolutionIn a triangle, the lengths of the two larger sides are 10 and 9, respectively. If the angles are in A.P, then the length of the third side can be (a) 5−√6 (b) 3√3 (c) 5 (d) 5+√6
View SolutionIn a triangle, the lengths of the two larger sides are 10 and 9, respectively. If the angles are in A.P., then the length of the third side can be 5−√6 (b) 3√3 (c) 5 (d) 5+√6
View SolutionIn a triangle PQR, let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE ?
View SolutionThe ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal, is (a) π :√2 (b) π :√3 (c) √3 :π (d) √2 :π
View SolutionIf the equation of base of an equilateral triangle is 2x−y=1 and the vertex is (−1,2), then the length of the sides of the triangle is (a)√203 (b) 2√15 (c)√815 (d) √152
View SolutionIf an equilateral triangle is inscribed in the circle x2+y2−6x−4y+5=0 then its side is
View Solution