Let f(x)=x−[x] , for every real number x (where, [x] is integral part of x). Then , the value of ∫1−1f(x)dx is equal to
1
2
0
1/2
The correct Answer is:A
We have,
1∫−1(x−[x])dx=0∫−1(x−[x])dx+1∫0(x−[x])dx
1∫−1(x−[x])dx=0∫−1(x+1)dx+1∫0(x−0)dx
1∫−1(x−[x])dx=[(x+1)22]0−1+[x22]10=12+12=1
ALTER It is evident from the graph of y=f(x) that
1∫−1dx=Area of ΔOLA+Area of ΔOMB
⇒1∫−1f(x)dx=2(Area ofΔOMB)
⇒1∫−1f(x)dx=2×12(OM×MB)=1×1=1
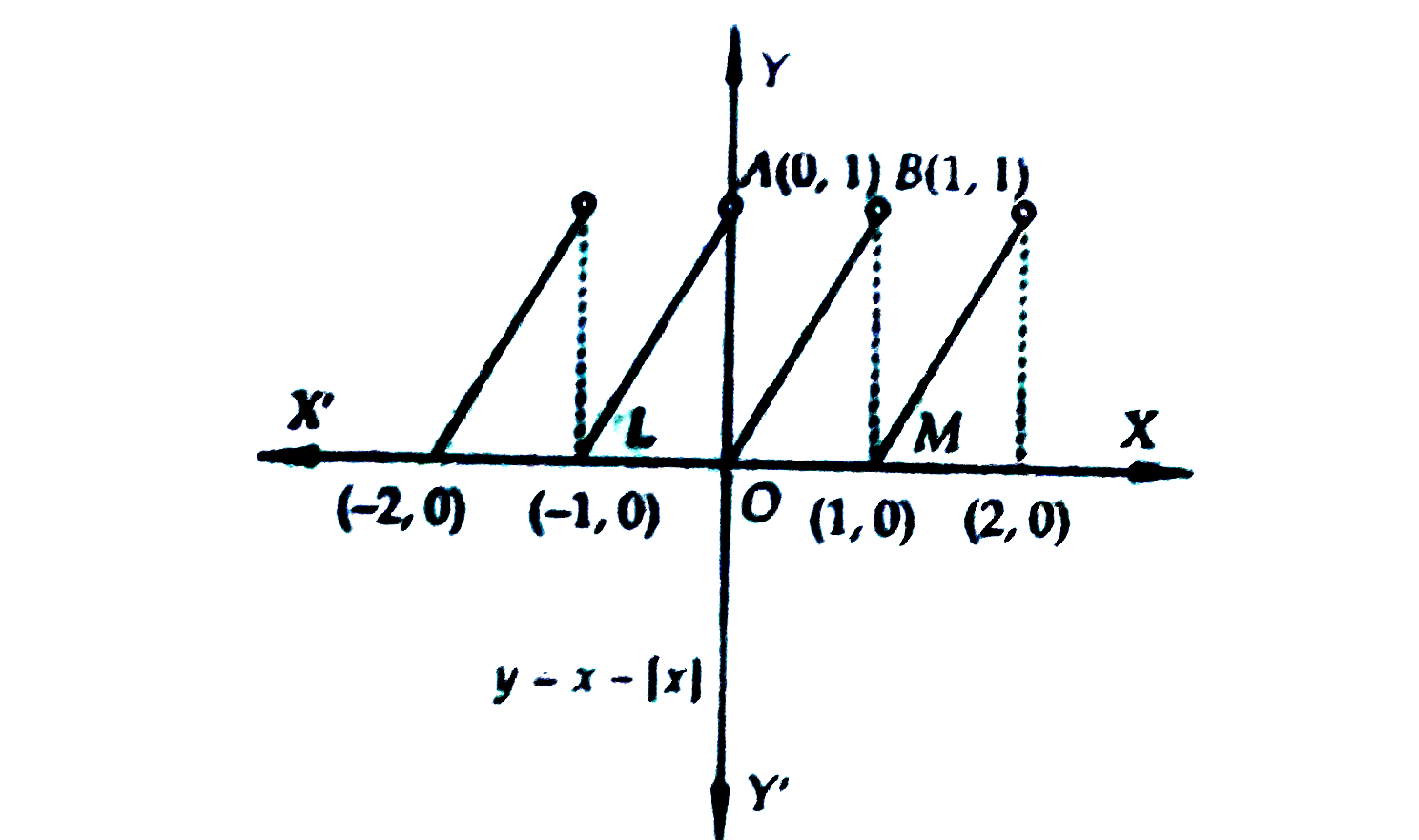
Topper's Solved these Questions
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Section I - Solved Mcqs
145 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type
12 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
Similar Questions
Let f(x)=x−[x], for every real number x, where [x] is integral part of x. Then ∫1−1f(x)dx is
View SolutionLet f(x)=x−[x], for ever real number x,where[x] is the greatest integer less than or equal to x. Then, evaluate ∫1−1f(x)dx .
View SolutionIf f(x)=min{|x−1|,|x|,|x+1|, then the value of ∫1−1f(x)dx is equal to
View SolutionLet f(n)=[12+n100] where [x] denote the integral part of x. Then the value of 100∑n=1f(n) is
View SolutionIf f(k−x)+f(x)=sinx, then the value of integral I=∫k0f(x)dx is equal to
View SolutionLet h(x)=f(x)−a(f(x))3 for every real number x
h(x) increase as f(x) increses for all real values of x if
View SolutionLet f(x)=limn→∞cosx1+(tan−1x)n. Then the value of ∫∞of(x)dx is equal to
View SolutionThe value of the integral ∫2a0f(x)f(x)+f(2a−x)dx is equal to
View SolutionIf f(x)=cos(tan−1x), then the value of the integral ∫10xf''(x)dx is
View SolutionIf f(x)=min({x},{−x})x∈R, where {x} denotes the fractional part of x, then ∫100−100f(x)dx is
View Solution
