Let f(x)=|x−x1|+|x−x2| where x1 and x2 are disinct real numbers of points at which f(x) is mimum is
More than 3
1
2
3
The correct Answer is:A
The graph of f(x) is shown in Fig 1. It is evident from the graph of f(x) that it attains mimimum values at every point in [x1,x2]
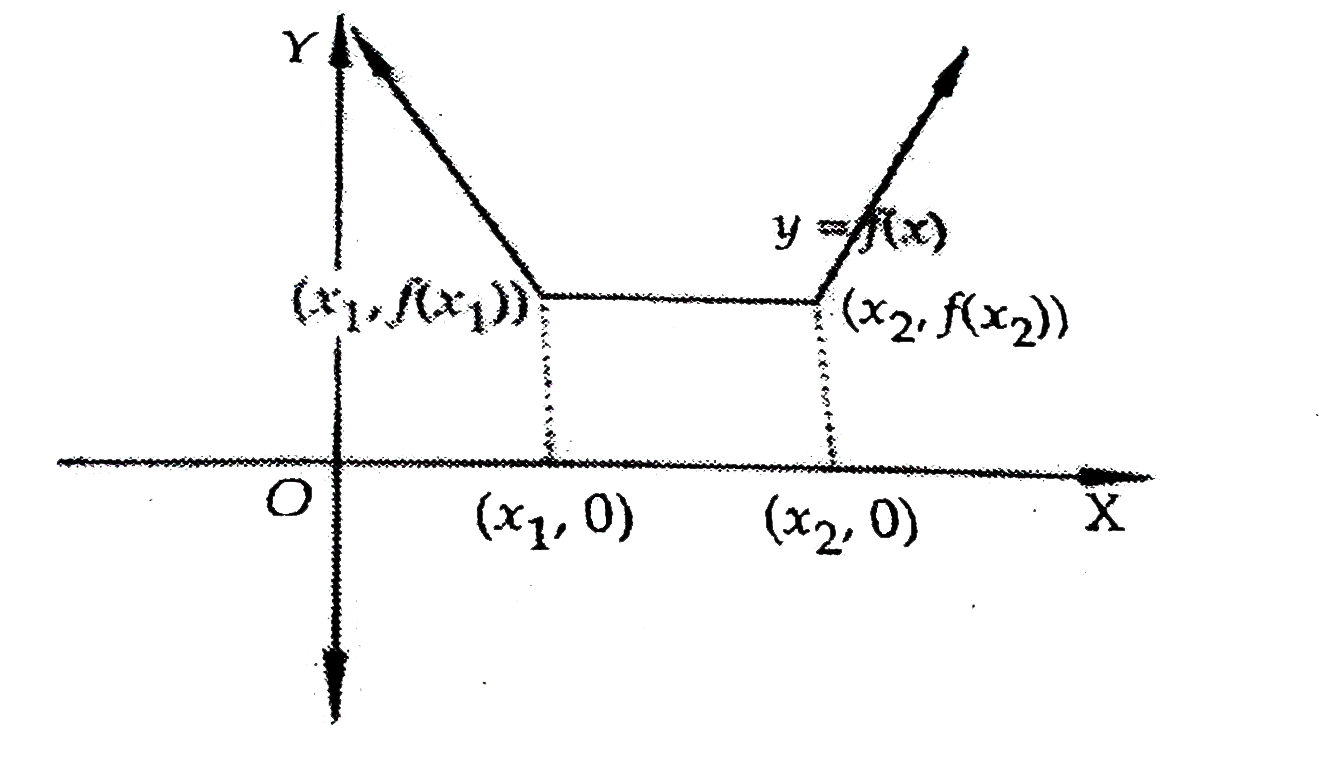
Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Section I - Solved Mcqs
72 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Section II - Assertion Reason Type
7 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test
20 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
Similar Questions
Let f(x)=x2−2x−1∀ξnR Let f:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective. If f:R→R , g(x)=f(x)+3x−1 , then the least value of function y=g(|x|) is
View SolutionLet f(x) be given that f(x)={xif x is rational1−xif x is irrational
The number of points at which f(x) is continuous, is
View SolutionLet f(x)=max.{∣∣x2−2∣∣x|∣,|x∣} then number of points where f(x) is non derivable, is :
View SolutionLetf(x)=⎧⎨⎩[x]−2≤x≤−122x2−1−12<x≤2andg(x)=f(|x|)+|f(x)|, where [.] represents the greatest integer function .
the number of point where g(x) is discontinuous is
View SolutionLetf(x)=⎧⎨⎩[x]−2≤x≤−122x2−1−12<x≤2andg(x)=f(|x|)+|f(x)|, where [.] represents the greatest integer function .
the number of point where |f(x)| is non - differentiable is
View SolutionLetf(x)=⎧⎨⎩[x]−2≤x≤−122x2−1−12<x≤2andg(x)=f(|x|)+|f(x)|, where [.] represents the greatest integer function .
the number of point where g(x) is non - differentiable is
View SolutionLet g(x)=(f(x))2+f(x)+19 where f(x)=|x−2|2+|x−2|−2 then number of single digit natural number of the range of g(x) is
View SolutionThe set of points, where f(x)= x1+∣x∣ is differentiable, is
View SolutionLet f(x)=x−[x], for every real number x, where [x] is integral part of x. Then ∫1−1f(x)dx is
View SolutionLet f(x)=x(x−1)2, find the point at which f(x) assumes maximum and minimum.
View Solution
