Find the equation of the ellipse whose focus is (1,0), the directrix is x+y+1=0 and eccentricity is equal to 1√2.
(x−1)2+y2=(x+y+1)2
2∣∣(x−1)2+Y2∣∣=(x+y+1)2
4{(x−1)2+y2}=(x+y+1)2
none of these
The correct Answer is:A
Let S(1,0) be the focus and ZZ' be the directrix let P(x,y) be any point on the ellipse and PM be perpendicular from P on directrix . Then by definition , we have .
SP=ePM, where e=1/√2
⇒SP2=e2PM2
⇒(x−1)2+(y−0)2=(1√2)2{x+y+1√1+1}2
⇒4{(x−1)2+y2}=(x+y+1)2
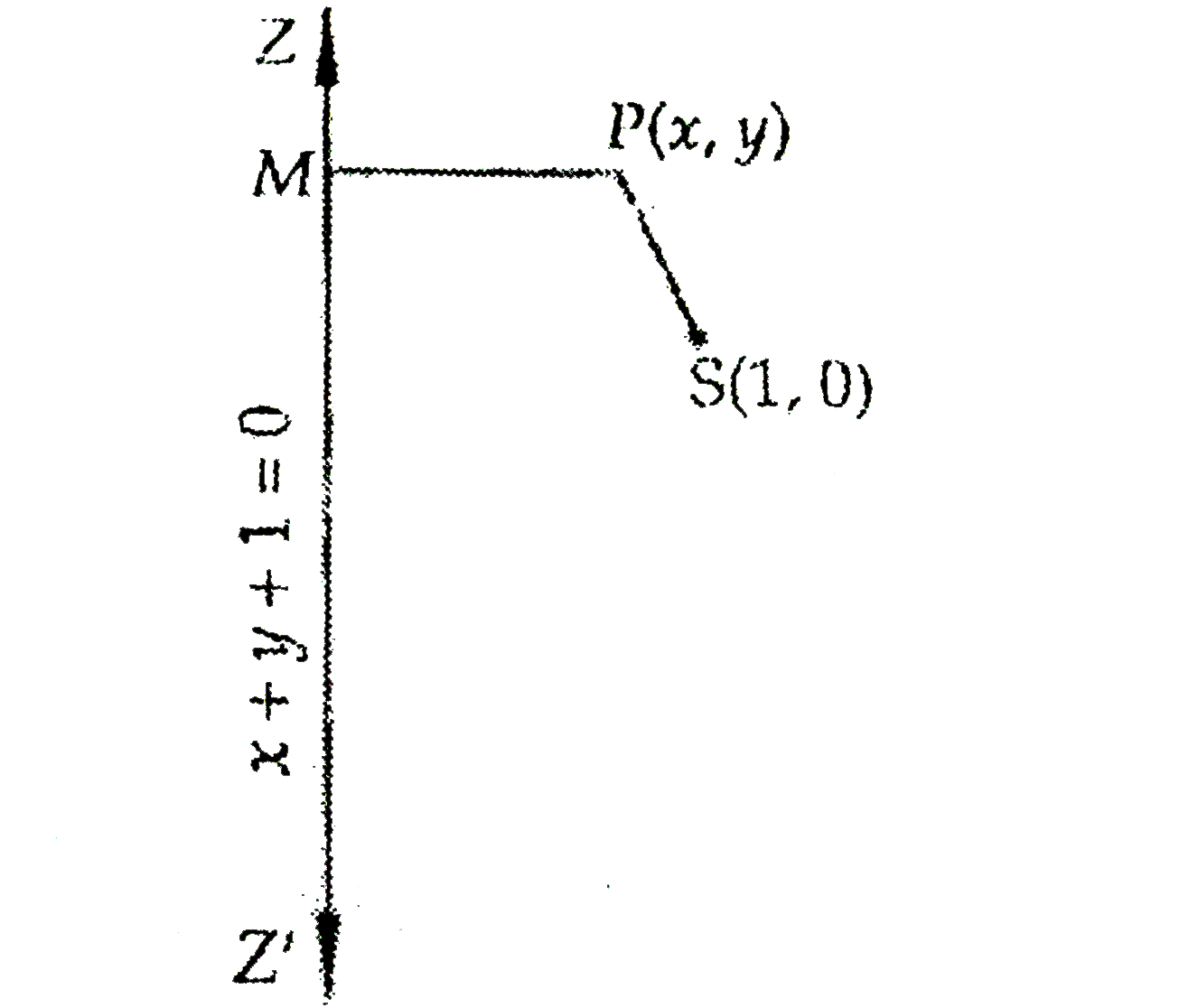
Topper's Solved these Questions
- ELLIPSEBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ELLIPSEEXERCISE - Section I - Solved Mcqs
59 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ELLIPSEEXERCISE - Section II - Assertion Reason Type
7 Videos
- DIFFERENTIATIONBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test
30 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
Similar Questions
Find the equation of the ellipse whose focus is (1,0), the directrix is x+y+1=0 and eccentricity is equal to 1√2.
View SolutionFind the equation of the ellipse whose focus is (1,-2) the directrix 3x−2y+5=0 and eccentricity equal to 1/2.
View SolutionFind equation of the ellipse whose focus is (1,-1), then directrix the line x-y-3=0 and eccentricity 12 is
View SolutionFind the equation to the ellipse whose one focus is (2, 1), the directrix is 2x−y+3=0 and the eccentricity is 1√2
View SolutionFind the equation to the ellipse whose one focus is (2,1), the directrix is 2x−y+3=0 and the eccentricity is 1√2.
View SolutionFind the equation of the hyperbola whose : focus is (1,1) directrix is 3x+4y+8=0 and eccentricity =2
View SolutionFind the equation of the hyperbola whose : focus is (0,3) directrix is x+y−1=0 and eccentricity =2.
View SolutionFind the equation of the ellipse whose : One focus is (6,7), directrix is x+y+2 and eccentricity is 1√3
View SolutionFind the equation of the hyperbola whose : focus is (1,1) directrix is 2x+y=1 and eccentricity =√3
View SolutionFind the equation of the hyperbola whose focus is (1,2), directrix 2x+y=1and eccentricity √3.
View Solution
