Question

A point moves so that the sum of the squares of
its distances from two intersecting straight lines is constant. Prove that
its locus is an ellipse.

Options

A. a pair of straight lines
B. a parabola
C. an ellipse
D. a hyperbola

Explanation

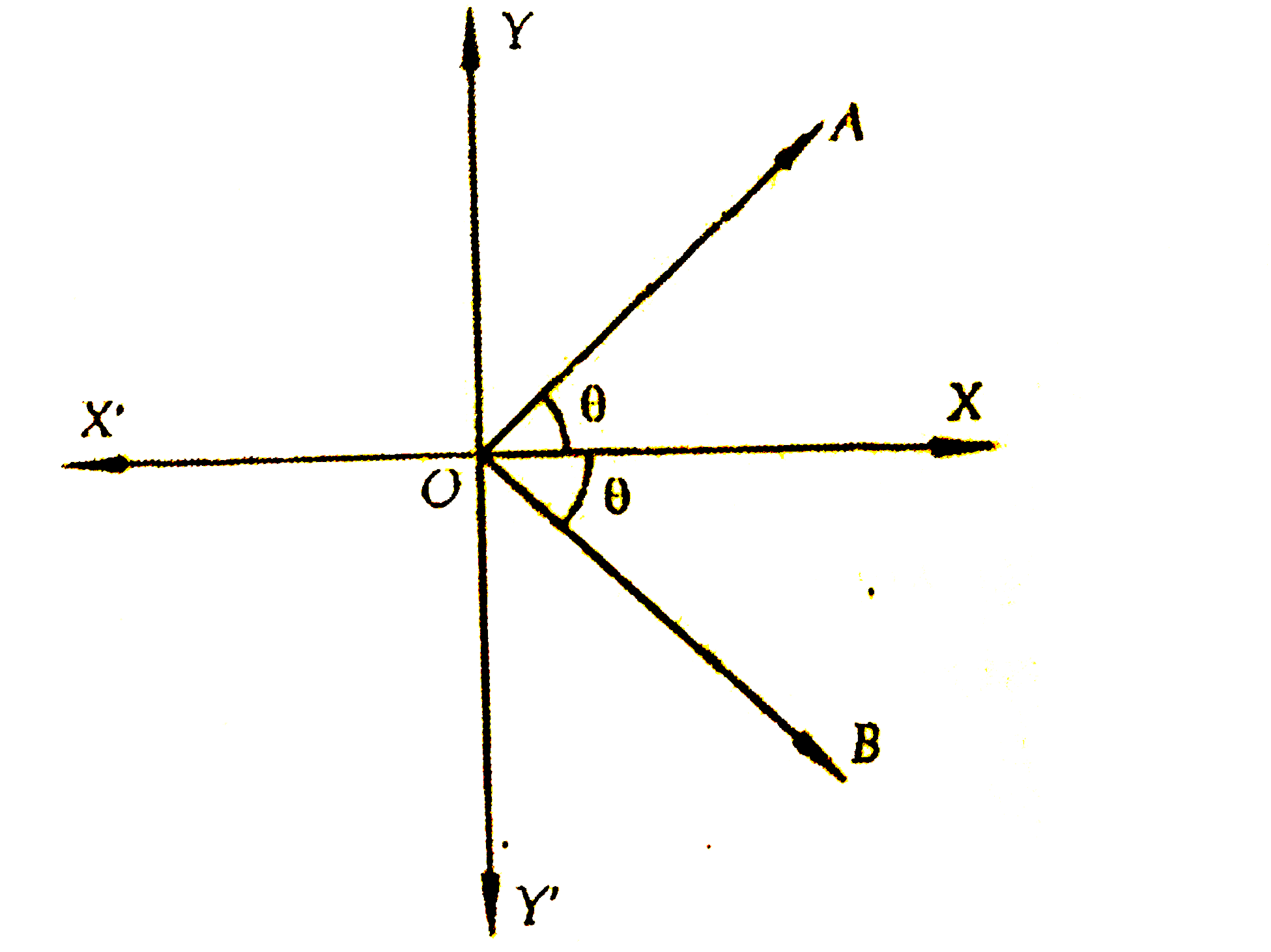
Let OA and OB be two intersecting lines containing an angle ` 2 theta ` between them .
Let OX and OY be the bisectors of angle between these lines taking OX and OY as the coordinate axes , the equations of OA and OB are y= x tan `theta and y =-x` tan `theta ` respectively
Let P(h,k) be a variable point such that the sum squares of its distance from OA and OB is contant equal to` lamda ^(2)` .
`i.e., {(|h sin theta -Kcos theta |)/sqrt(sin ^(2) theta + cos ^(2)theta )}^(2) +{(|h sin theta +k cos theta |)/(sqrt(sin ^(2)theta+ cos ^(2) theta))}^(2) = lamda^(2)`

`implies 2h^(2) sin ^(2) theta+2k^(2)cos^(2)theta = lamda^(2)`
hence , the locus of (h,k) is
`2x^(2) sin ^(2) theta = lamda ^(2) or , (x^(2))/(((lamda^(2))/(2)cosec^(2)theta )+(y^(2))/((lamda^(2))/(2)sec^(2) theta )= 1 `
Clearly , it represents an ellipse .\