Question

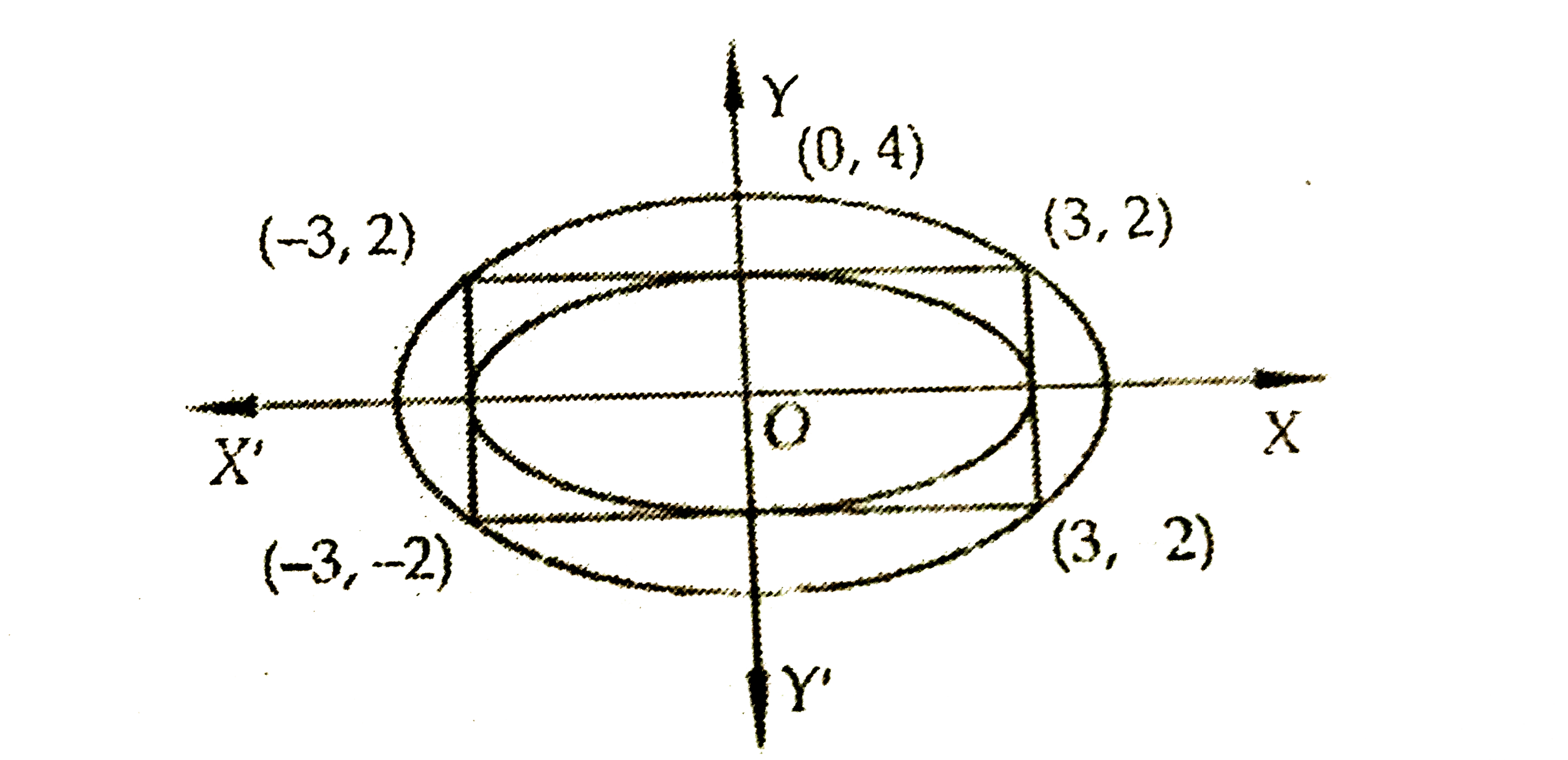
The ellipse $E_1:\frac{x^2}{9}+\frac{y^2}{4}=1$
is inscribed in a rectangle $R$
whose sides are parallel to the coordinate axes. Another ellipse $E_2$
passing through the point (0, 4) circumscribes the rectangle $R\stackrel{.}{}$
The eccentricity of the ellipse $E_2$
is
$\frac{\sqrt{2}}{2}$
(b) $\frac{\sqrt{3}}{2}$
(c) $\frac{1}{2}$
(d) $\frac{3}{4}$

Options

A. `(sqrt(2))/(2)`
B. `(sqrt(3))/(2)`
C. `(1)/(2)`
D. `(3)/(4)`

Answer

C

Explanation

Let the equation of the ellipse `E_(2) be (x^(2))/(a^(2))+(Y^(2))/(b^(2))=1.`
it passes through (3,2) and (0,4)
`therefore (9)/(a^(2))+(4)/(b^(2))=1 and (16)/(b^(2))=1`
`implies b=4 and a^(2)=12`
let e be the eccentricity of ellipse `E_(2)` then ,
`e=sqrt(1-(a^(2))/(b^(2)))=sqrt(1-(12)/(16))=(1)/(2)`
ALITER the equation of second degree curve passing through the intersection of `x=3 , x=-3,y=2 and y=-2` is
`(x+3)(x-3)+ lamda(y+2)(y-2)=0`
it passes through (0,4)
`therefore -9+12 lamda =0implies lamda=(3)/(4)`
ltbrlt puting ` lamda =(3)/(4) ` in (i) we get 4x^(2)+3y^(2)=48 or ,(x^(2))/(12)+(y^(2))/(16)=1`
let e be eccentricity , then `e=sqrt(1-(12)/(16))=(1)/(2)`