Question

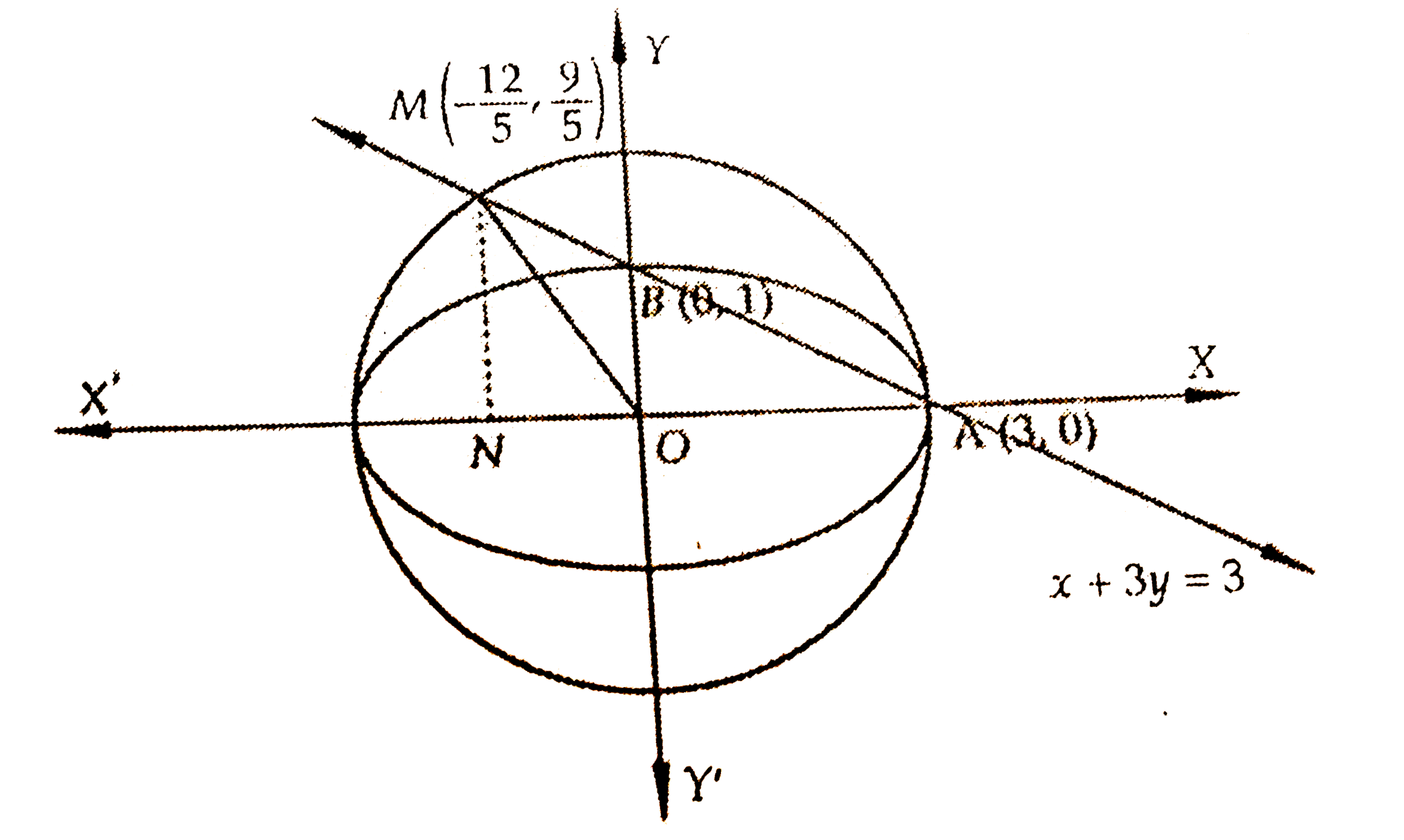
The line passing through the extremity $A$
of the major exis and extremity $B$
of the minor axis of the ellipse $x^2+9y^2=9$
meets is auxiliary circle at the point $M\stackrel{.}{}$
Then the area of the triangle with vertices at $A,M,$
and $O$
(the origin) is
(a) 31/10 (b) 29/10 (c) 21/10
(d) 27/10

Options

A. `31//10`
B. `29//10`
C. `21//10`
D. `27//10`

Answer

D

Explanation

The coordinate of A and B are (3,0) and (0,1) respectivley the auxiliary circle is `x^(2)+y^(2)=9`
Equation of line AB is `(x)/(3)+(y)/(1) =1 or x+3y=3` this cuts the auxiliary circle at `M(-12//5,9//5)`
` therefore ` Area of `Delta AOM =(1)/(2) xxOA xxMN =(1)/(2) xx3xx(9)/(5)=(27)/(10)`